如何使用Excel計算偏態和峰態

在行為和社會科學的領域裡，常態分配（normal distribution）是很常見的次數分配形狀，最顯著的特徵為酷似大鐘的曲線和從中間劃分為左右對稱的分配。相較於常態分配，偏態（skew）和峰態（kurtosis）則是偏離常態的次數分配形狀，雖然可能較少見或偏離常態的幅度不大，但在描述資料整體的分布情況時，仍舊是值得參考的數據。

若有 SPSS，要取得偏態和峰態的數值並不困難，只要透過敘述統計分析下的次數分配表或敘述統計，皆有峰態和偏態的選項可勾選。但若沒有 SPSS 或其他的統計分析軟體，也可以使用微軟的 Excel 來計算偏態和峰態的數值，而且操作上相當地簡單。

由於本篇文章主要探討如何透過 Excel 取得偏態和峰態的數值，若您不明瞭或不熟悉偏態和峰態的意義，建議您先閱讀次數分配的形狀：常態、偏態和峰態，將有助於以下文章內容的理解。

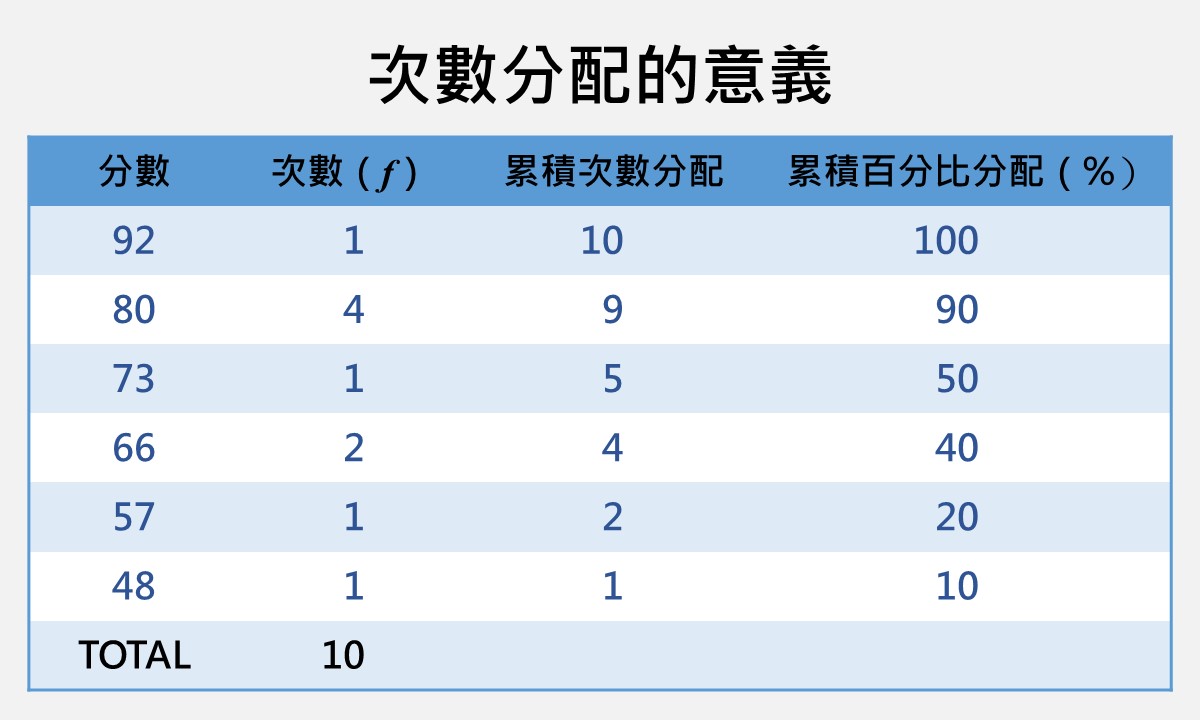
以下使用分組分數次數分配裡50位學生的成績當作樣本資料，分別示範如何使用Excel計算偏態和峰態的數值，並說明數值所代表的意義。

使用 Excel 計算偏態
使用 Excel 計算峰態

使用 Excel 計算偏態

偏態分配指分數的次數分配不是左右對稱的形狀，而是多數的分數集中在低分或高分的一側，另一側的分數次數則慢慢地減少，因此偏態可說是測量不對稱的程度。當多數的分數集中在低分的一側，且隨著分數愈高次數愈少時，稱為正偏態（positively skewed）；反觀，當多數的分數集中在高分的一側，且隨著分數愈低次數愈少時，則稱為負偏態（negatively skewed）。

用來計算偏態的 Excel 函數為 SKEW，其語法為 SKEW(number1, [number2], …)，括弧裡須指出想要求得偏態的資料範圍，可以逐一輸入分數或明確地指出資料所在的儲存格範圍。

讓 $n$ 為樣本總個數、 $x_i$ 指第 $i$ 個分數、 $\overline x$ 為平均數、 $s$ 為標準差，根據微軟的支援網站，SKEW 函數使用下面的公式來計算偏態的數值：

$\frac {n}{(n-1)(n-2)} \sum_{i=1}^{n} { \left ( \frac {x_i- \overline x}{s} \right )^3}$

從這個公式可以發現，樣本總個數 $n$ 須至少為3，且標準差 $s$ 不等於0的情況下，Excel 才能正確地計算出偏態的數值，否則會傳回「#DIV/0!」的錯誤訊息。

將分組分數次數分配裡50個分數輸入至Excel空白活頁簿裡，儲存格範圍從B2到B51。在任一空白的儲存格輸入 SKEW，代表偏態，並在這個儲存格的右邊儲存格輸入 =SKEW(B2:B51)，要求計算位在儲存格B2到B51的50個分數的偏態數值。

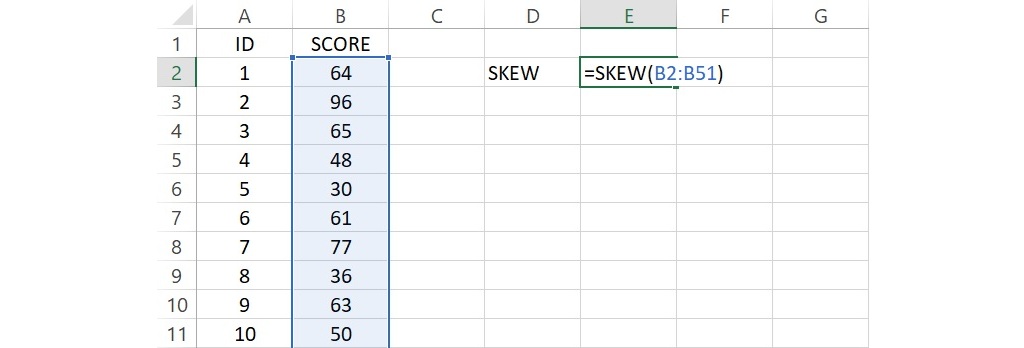
語法輸入完成後，按下 Enter 會傳回數值-0.036，此即為50個分數的偏態統計量。由於偏態的數值小於0，但只有些微地偏離0，代表這50個分數呈現略微的負偏態。

另一個在 Excel 裡偏態計算的函數為 SKEW.P，語法為 SKEW.P(number1, [number2], …)，括弧裡可逐一輸入分數或明確地指出資料所在的儲存格範圍。SKEW.P 函數和 SKEW 函數的不同之處在於，SKEW.P 函數用來計算母群體的偏態數值而 SKEW 函數用來計算樣本的偏態數值。

讓 $N$ 為母群體總個數、 $X_i$ 指第 $i$ 個分數、 $\mu$ 為母群體平均數、 $\sigma$ 為母群體標準差，SKEW.P 函數使用下面的公式來計算母群體的偏態數值：

$\frac {1}{N} \sum_{i=1}^{N} { \left ( \frac {X_i- \mu}{\sigma} \right )^3}$

假設上面的50個分數為母群體的分數，在任一空白儲存格輸入 SKEW.P，代表母群體的偏態，並在這個儲存格的右邊儲存格輸入 =SKEW.P(B2:B51)，這個公式語法要求計算位於儲存格B2到B51的50個母群體分數的偏態數值。

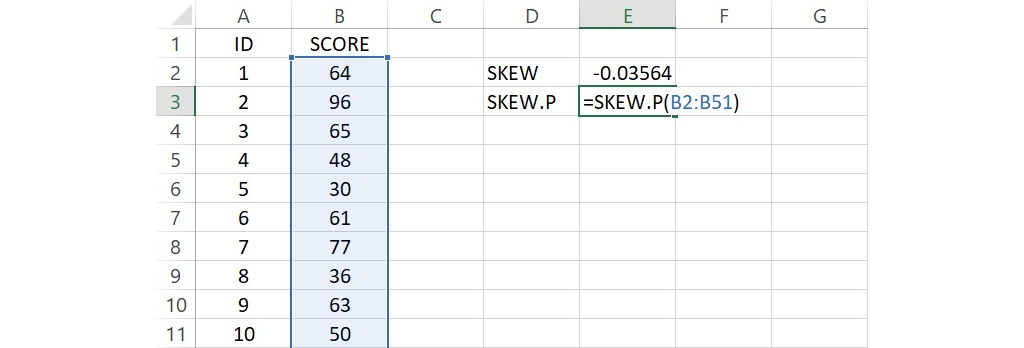
語法輸入完成後，按下 Enter 會傳回數值-0.035，這就是50個母群體分數的偏態數值。和上面樣本偏態數值的解釋相同，這50個母群體分數呈現少許的負偏態。

使用 Excel 計算峰態

峰態是指分數相對地集中在中間和尾端的程度，在常態分配下，落在兩側尾端和集中在中間的分數皆不會太多也不會太少，稱為常態峰（mesokurtic）。當較多的分數集中在兩側尾端和中間時，次數分配的曲線變得比較高聳和重尾，稱為高狹峰（leptokurtic）；反觀，當較少的分數落在兩側尾端和中間時，次數分配的曲線變得比較平坦和輕尾，則稱為低闊峰（platykurtic）。

Excel 用來計算峰態的函數為 KURT，其語法為 KURT(number1, [number2], …)，括弧裡須指出想要求得峰態的資料範圍，可以逐一輸入分數或明確地指出資料所在的儲存格範圍。

讓 $n$ 為樣本總個數、 $x_i$ 指第 $i$ 個分數、 $\overline x$ 為平均數、 $s$ 為標準差，根據微軟的支援網站，KURT 函數使用下面的公式來計算峰態的數值：

$\left \{ \frac {n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i=1}^{n} \left ( \frac {x_i-\overline x}{s} \right )^4 \right \} - \frac {3(n-1)^2}{(n-2)(n-3)}$

從上面的公式可以看出，樣本總個數 $n$ 須至少為4，且標準差不等於0的情況下，Excel 才能正確地計算出峰態的數值，否則 KURT 函數會傳回「#DIV/0!」的錯誤訊息。

同樣使用上面50個分數，在活頁簿裡的任一空白儲存格輸入 KURT，代表峰態，並在這個儲存格的右邊儲存格裡輸入 =KURT(B2:B51)，這個公式語法要求計算位於儲存格B2到B51的50個分數的峰態。

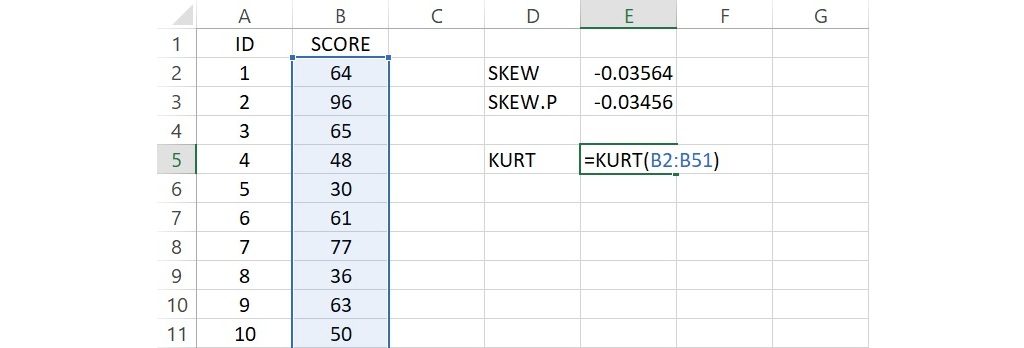
語法輸入完成後，按下 Enter 會傳回數值-0.915，此即為50個分數的峰態數值。因為峰態的數值小於0，所以次數分配呈現低闊峰。

KURT 函數用來取得樣本資料的峰態數值，不過至目前為止 Excel 並沒有提供可計算母群體峰態的函數。若想求得母群體的峰態數值，可先利用 KURT 函數計算出資料的峰態，再將該峰態數值帶入下面的公式（Zaiontz, 2023）：

(1) $\begin{equation*}\frac {\displaystyle \frac {\text {KURT()}(n-2)(n-3)}{n-1}-6}{n+1}\end{equation*}$

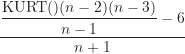
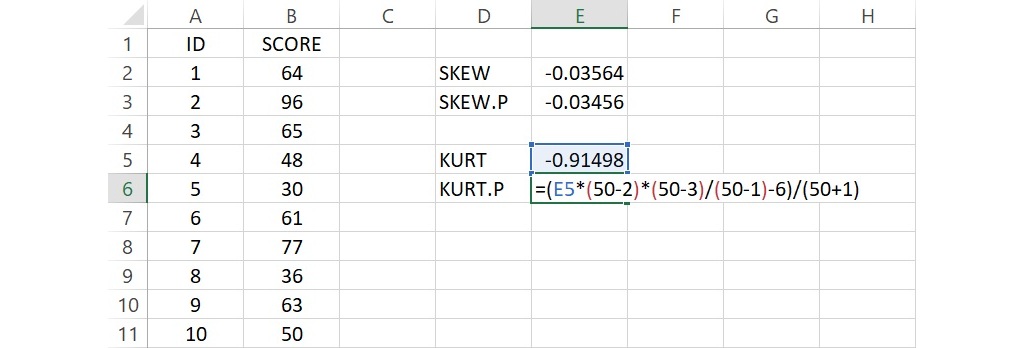
再次假設上面的50個分數為母群體的數值，已藉由 KURT 函數計算得到峰態數值為-0.915（儲存格E5）。接著，在任一空白儲存格輸入 KURT.P，代表母群體的峰態，並在這個儲存格右邊的儲存格裡輸入下面的公式語法：

=(E5*(50-2)*(50-3)/(50-1)-6)/(50+1)

這公式語法套用上面的公式(1)，輸入完成後，按下 Enter 會傳回數值-0.944，此即為母群體的峰態數值。因為數值為負數，所以這個母群體的分數呈現低闊峰，代表分配曲線的中間較為平坦，且兩側尾端為輕尾；換句話說，大多數的分數集中在中央和尾端之間的地方。

calculation of kurtosis for population in excel

母群體的峰態也可透過下面的公式來計算，得到的結果和使用上面公式(1)所獲得的結果是相同的。若您有興趣，可以計算看看喔！

$\left \{ \frac {1}{N} \sum_{i=1}^{N} { \left ( \frac {X_i- \mu}{\sigma} \right )^4} \right \} - 3$

從上面的計算結果可以發現，利用Excel取得的偏態和峰態兩個數值和在次數分配的形狀：常態、偏態和峰態裡運用 SPSS 查詢所獲得的結果是相同的。因此，在沒有 SPSS 或其他統計分析軟體的情況下，也可以使用 Excel 來進行相同的分析，而且操作上相當地簡單。

若您不熟悉上面內容提到的數學計算方法，可以參考如何使用 Excel 進行數學計算【基礎篇】和如何使用 Excel 進行數學計算【進階篇】。

以上為本篇文章對如何使用Excel來計算偏態和峰態的介紹，希望透過本篇文章，您瞭解了 SKEW 和 KURT 兩個函數的功能，並學會了如何利用這兩個函數來求得資料的偏態和峰態數值。若您喜歡本篇文章，請將本網站加入書籤，並持續回訪本網站喔！此外，也歡迎您追蹤本網站的 Facebook 和／或 X（Twitter）專頁喲！

如果您覺得本篇文章對您有幫助，歡迎買杯珍奶給 Dr. Fish！小小珍奶，大大鼓勵，您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔！

參考資料

Zaiontz, C. (2023). Symmetry, skewness and kurtosis. Real statistics using Excel. https://www.real-statistics.com/descriptive-statistics/symmetry-skewness-kurtosis/

使用 Excel 計算偏態

使用 Excel 計算峰態

參考資料

您可能也會喜歡