次數分配的形狀：常態、偏態和峰態

次數分配（frequency distribution）是指將一組資料裡的所有數值和每個數值出現的次數完整地顯示出來，通常會將數值從大至小排序，以表格的方式來呈現，而該表格即稱為次數分配表。更詳細的次數分配之說明，請參考次數分配的意義。

透過次數分配表，可讓數值整體的分布情形更為一目了然。次數分配可能會呈現出多種不同的形狀，在資料分析開始前，若能先瞭解資料分布的形狀，將有助於資料分析的過程和分析結果的解釋。以下將介紹幾種比較常見的分配形狀，並示範利用SPSS查詢這些分配形狀數值的方法。您可點選下方的任一連結，以便跳至您想閱讀的內容。

• 次數分配的形狀
  • 常態
  • 偏態
  • 峰態
• 運用SPSS查詢偏態和峰態的數值

次數分配的形狀

若依據資料分布是否左右對稱而言，次數分配的形狀可分為常態與偏態；若從分數集中在分配兩側尾端的程度來看，則可分為常態和峰態，以下分別探討。

常態

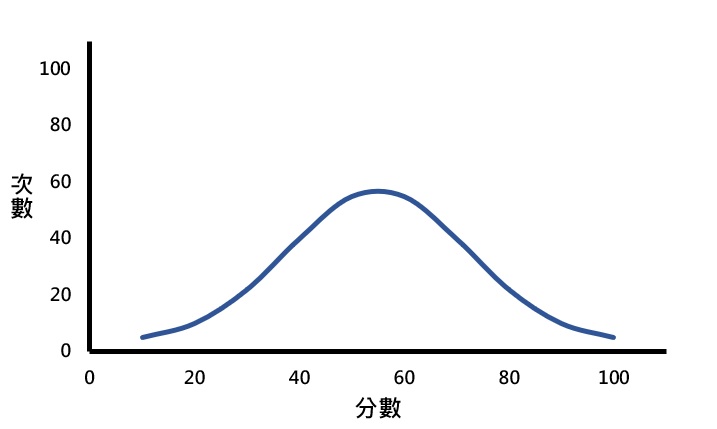
在一個完美的世界裡，數據資料會圍繞著中間的數值而展現出左右對稱的（symmetrical）分布型態，換句話說，若在分配的中間畫一條垂直線，該條線左右兩邊的形狀是一模一樣的，如下圖所示。由於此種對稱曲線的形狀類似一個大鐘，所以也被稱為鐘形曲線（bell-shaped curve），而此種形狀的分配則稱為常態分配（normal distribution）。

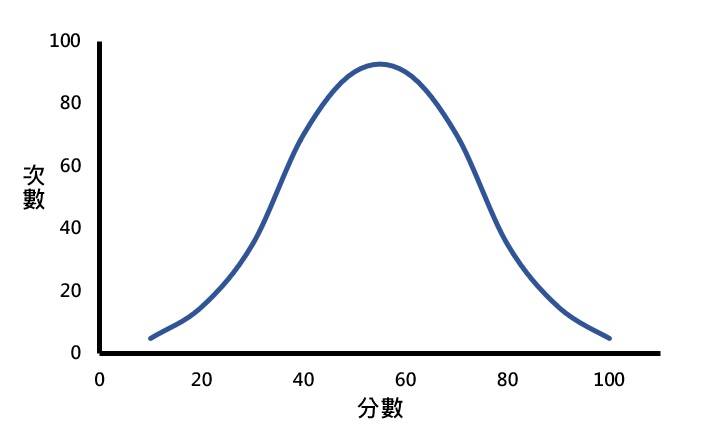
從常態分配曲線（鐘形曲線）的形狀可看出該條曲線是左右對稱的，而且大多數的分數落在分配的中間。當慢慢地從中間往兩側移動時，分數的次數會漸漸地減少；離中間愈遠時，分數的次數會愈少。

偏態

當次數分配不是左右對稱的形狀時，稱為偏態（skew）。偏態分配的典型特徵是多數的分數集中在低分或高分的一側，而在另一側的分數次數則慢慢地減少。若多數的分數集中在低分的一側，且分數愈高次數愈少時，稱為正偏態（positively skewed），如下圖。

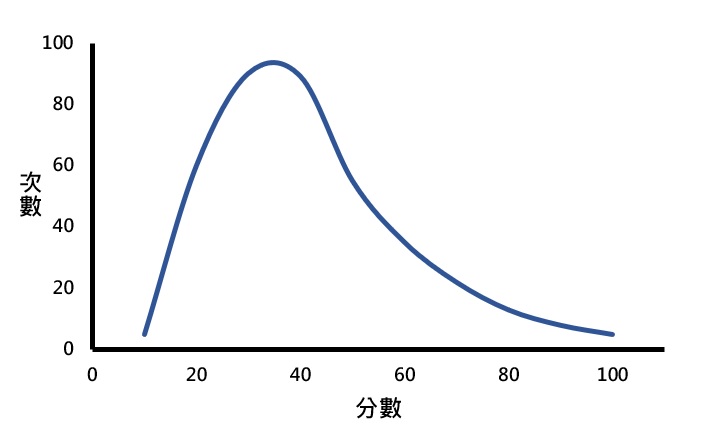
反過來看，若多數的分數集中在高分的一側，且分數愈低次數愈少時，稱為負偏態（negatively skewed），如下圖。

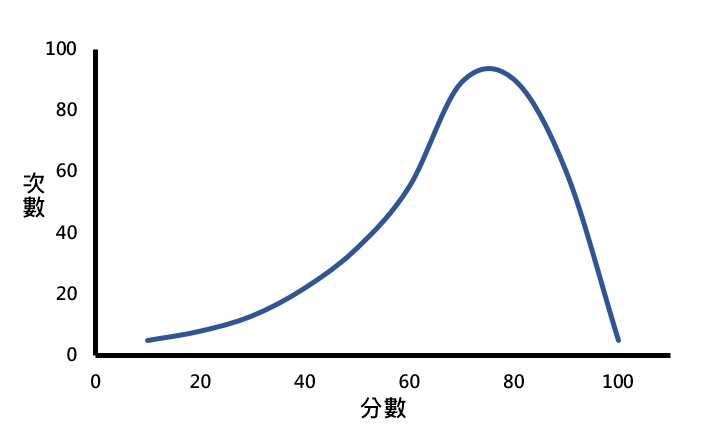
除了偏態分配之外，峰態（kurtosis）也會影響次數分配的形狀，有高狹峰和低闊峰之分，以下來介紹。

峰態

峰態是指相較於常態分配，分數集中在分配兩側尾端的程度，通常從分配的尖銳程度來判斷。與常態分配相比，若分配帶有較高聳的尖峰，並且有較多的分數落在分配兩側的尾端時，也就是重尾（heavy-tailed）分配或離群值（outlier）較多的情況，稱為高狹峰（leptokurtic）。

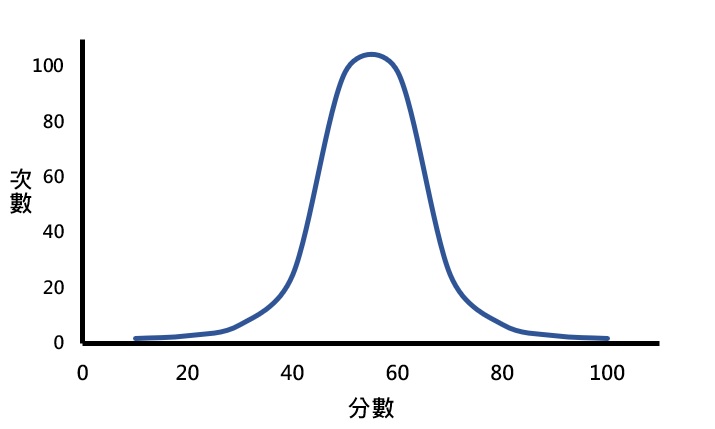
反過來看，若分配的尖峰較常態分配平坦，且較少分數落在分配兩側的尾端，也就是輕尾（light-tailed）分配或離群值較少的情況時，則稱為低闊峰（platykurtic）。

瞭解了常見的次數分配形狀之後，接著來看看如何利用SPSS找到偏態和峰態數值的方式，以及如何評估這些數值。

運用SPSS查詢偏態和峰態的數值

在理想的狀態下，常態分配的偏態和峰態的數值皆為0，但現實生活中，偏態和峰態皆不存在的情況微乎其微。若想知道偏態和峰態的數值，可利用SPSS來查詢，有兩種方法，以下使用分組分數次數分配文章裡50位學生的成績來示範。

方法1

將50位學生的成績輸入至SPSS資料編輯器裡，點選功能表的分析 » 敘述統計 » 次數分配表，帶出「次數分配表」視窗。關於SPSS資料輸入的方法，請參考SPSS操作環境和資料輸入。

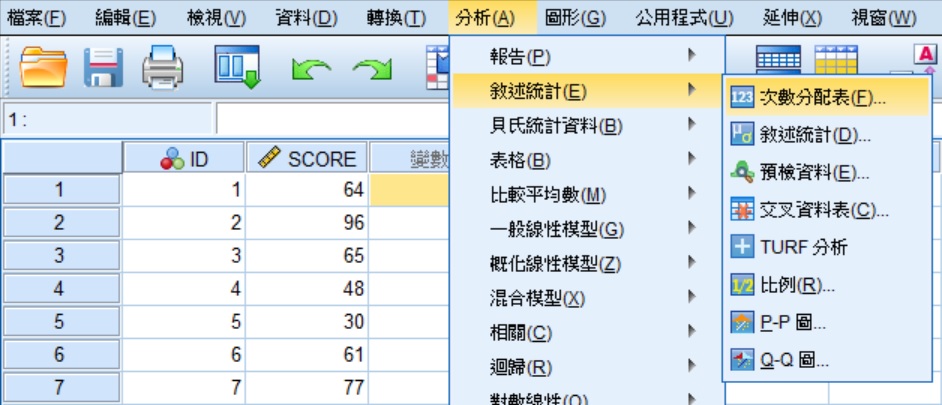
在「次數分配表」視窗中，將變項SCORE移到變數(V)方框中，再點選右邊的統計資料(S)，會出現「次數：統計量」視窗。在該視窗的右下方，勾選以事後分佈為特徵(Z)方框裡的偏態(W)和峰態(K)，按下繼續(C)，回到「次數分配表」視窗後，再按下確定。

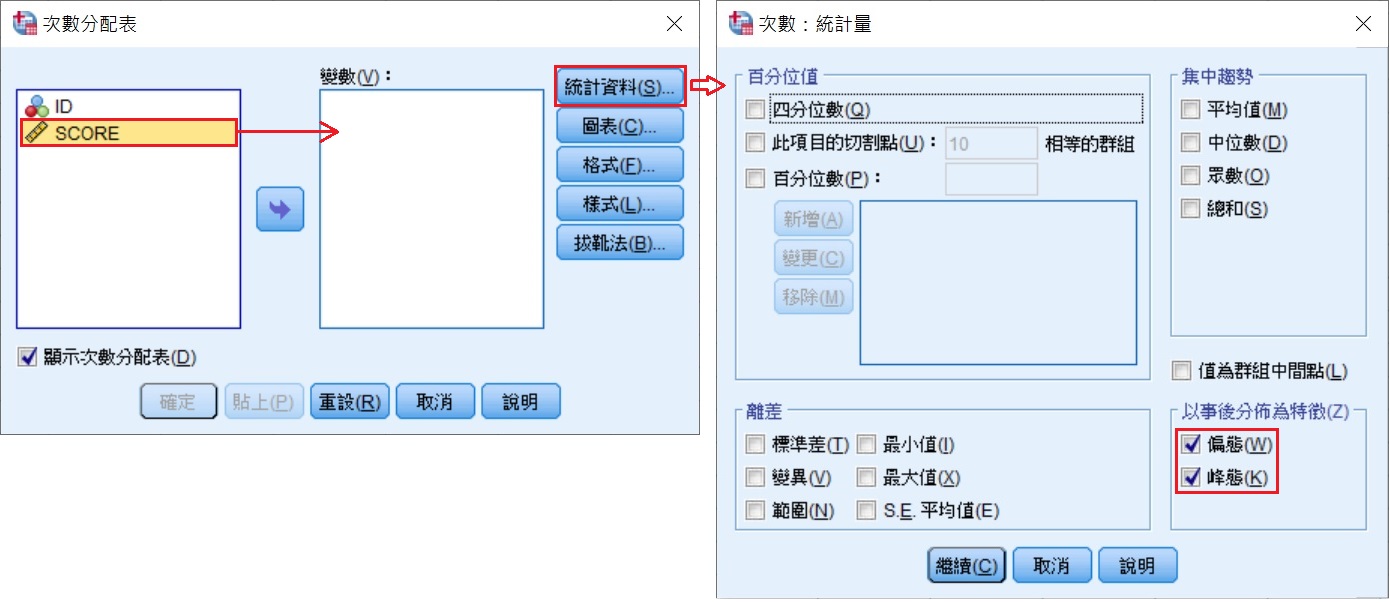
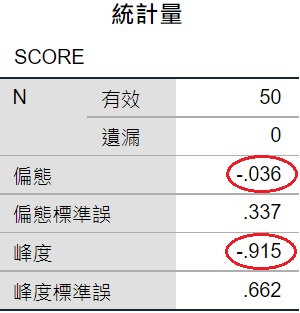
下表為SPSS輸出的資訊，顯示這50位學生成績的偏態數值為-0.036，峰度（也就是峰態）數值為-0.915。

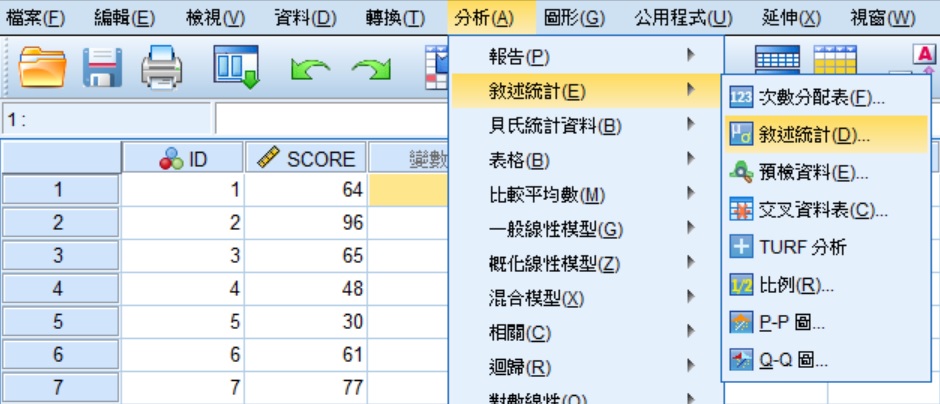
方法2

在已經輸入50位學生成績的SPSS資料編輯器頁面，點選功能表的分析 » 敘述統計 » 敘述統計，帶出「敘述統計」的視窗。

在「敘述統計」視窗中，將變項SCORE移至變數(V)的方框中，再點選右邊的選項(O)，於隨即出現的「敘述統計：選項」視窗中，勾選以事後分佈為特徵(Z)方框中的峰態(K)與偏態(W)，按下繼續(C)，回到「敘述統計」視窗後，再按下最下方的確定。

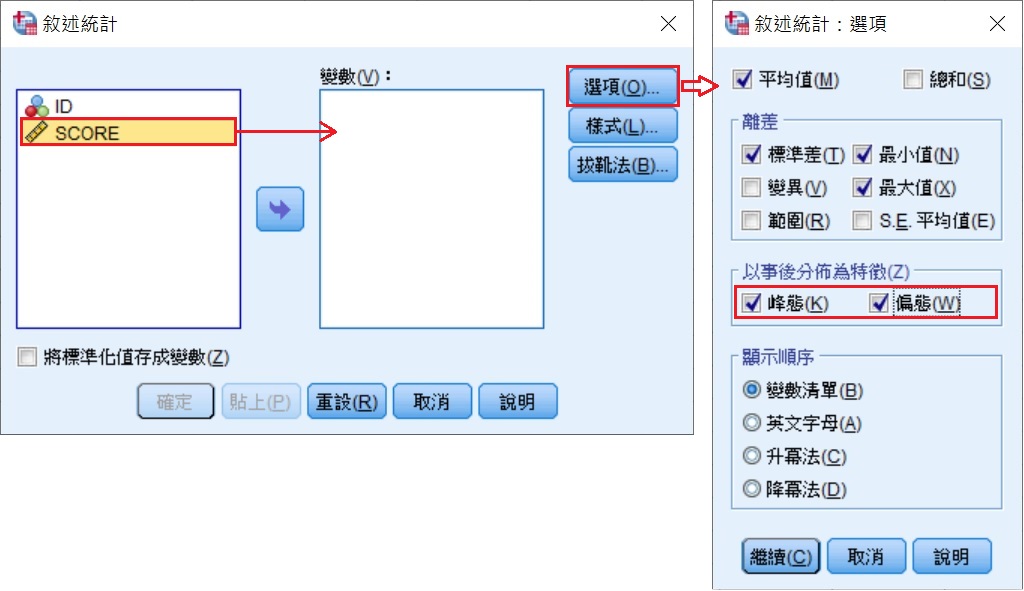
透過此方法，SPSS會輸出如下表的資訊。從下表可看出，50位學生成績的偏態數值為-0.036，峰態數值為-0.915，和上面方法1所輸出的數值是相同的。

不論是偏態或峰態，當數值不等於0時，即代表著偏離常態的分配。對於偏態而言，大於0表示正偏態，小於0表示負偏態；對於峰態而言，大於0代表高狹峰，小於0代表低闊峰。這裡SPSS的輸出結果顯示偏態數值為-0.036，峰態數值為-0.915，代表學生的成績呈現些微負偏態和低闊峰。

雖然理論上而言，只要偏態或峰態的數值不等於0，即是偏離常態的分配，但現實生活中蒐集到的資料，不太可能呈現完美的常態分配，因此何種程度的偏態或峰態才屬於實質上偏離常態呢？有學者指出，若偏態的數值大於1或小於-1，實質上即可被視為偏態分配；同樣地，若峰態數值大於1，代表分配過於高聳，小於-1則代表分配過於平坦（Hair et al., 2017, p61），您可將這些標準作為參考。

若您沒有SPSS或其他的統計分析軟體，但想求得偏態或峰態的數值時，也可以使用微軟的Excel來計算，詳細的操作方法請參考如何使用Excel計算偏態和峰態。

以上為本篇文章對於常見的次數分配形狀之介紹，希望透過本篇文章，您瞭解了常態、偏態和峰態分配的形狀和特徵，也學會了如何運用SPSS尋找偏態和峰態的數值。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站喔！另外，也歡迎按讚和追蹤我們的Facebook和Twitter專頁喲！

參考資料

Hair, J. F., Hult, G. T. M., Ringle, C., & Sarstedt, M. (2017). A primer on partial least squares structural equation modeling (PLS-SEM) (2nd ed.). SAGE Publications.