集中趨勢測量和偏態分配的關係

整理數據資料時，可以製作次數分配表（請參考次數分配的意義和分組分數次數分配）和繪製圖形來觀察數值整體的分布情況。若想用一個數值代表數值整體的分布狀態或進行跨分配間的比較，則可計算眾數、中位數和平均數這3個集中趨勢的統計量。關於眾數、中位數和平均數的詳細介紹，請參考集中趨勢的測量。

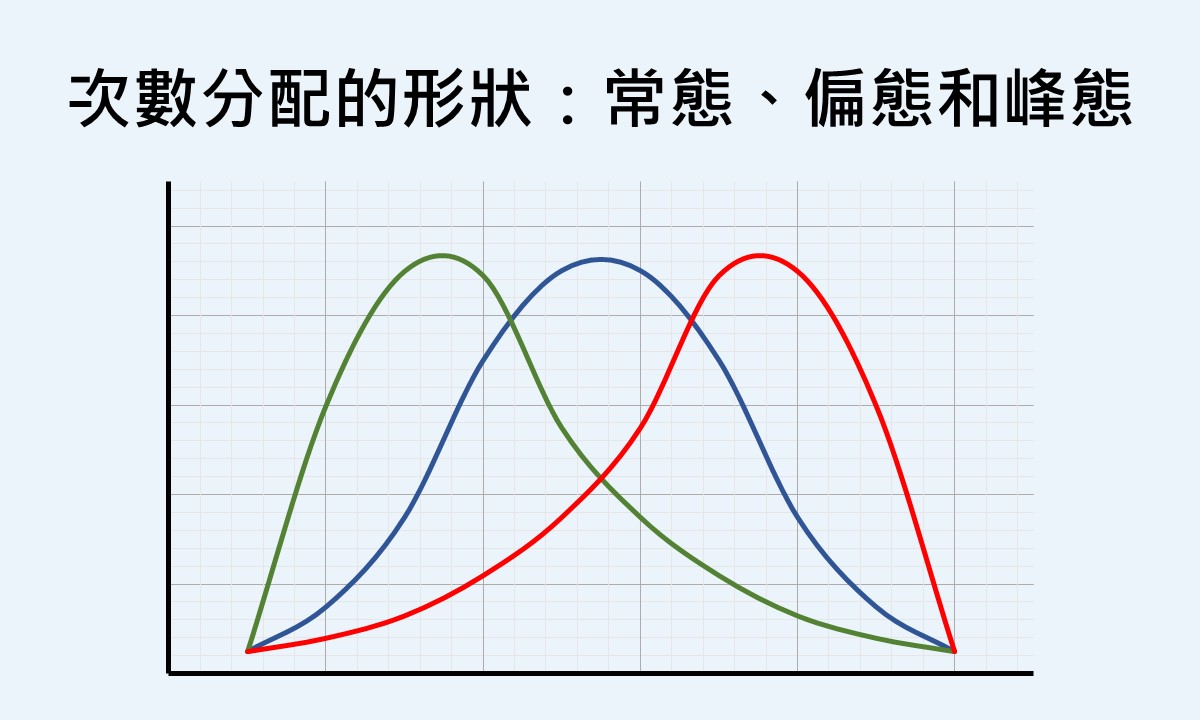
若從數據資料的分布是否左右對稱來看，分布型態可分為常態分配（normal distribution）和偏態分配（skewed distribution），且眾數、中位數和平均數等集中趨勢測量的相對位置會因為不同的分布型態而有所變化。

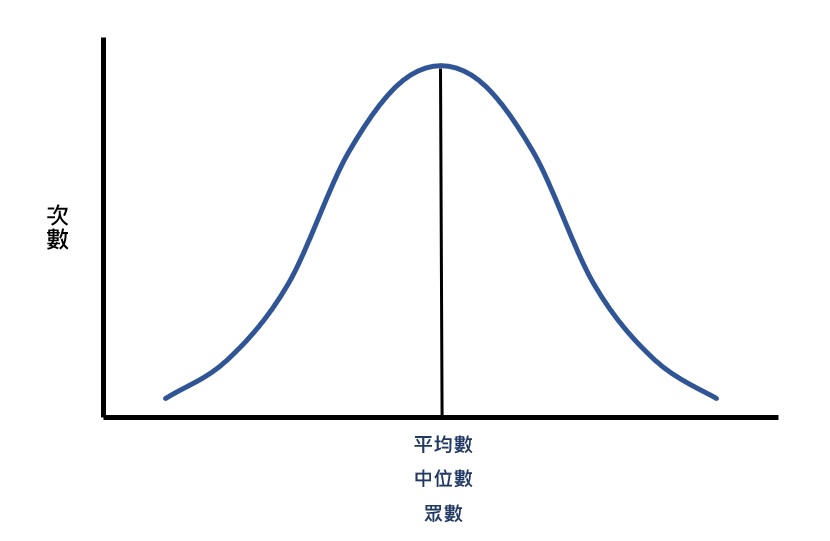
在理想的狀態下，數據資料會圍繞著中間的數值而呈現對稱的（symmetrical）分布型態，離中間愈遠，數值變得愈少，即為常態分配。由於其外觀很像一座大鐘，所以又稱為鐘形曲線（bell-shaped curve）。很多社會和行為科學的變項都具有常態分配的分布型態，例如身高、體重、考試成績、智力。

在常態分配下，眾數、中位數和平均數這3個集中趨勢測量的統計量都是相同的數值，如下圖所示：

不過在現實生活中，很多的數據資料並非呈現對稱的分布型態，而是偏態的分配。偏態分配的數值會大多集中於低分或高分之一側，而另一側的數值次數則會朝著分配的尾端慢慢地減少，藉此區分為正偏態（positively skew）與負偏態（negatively skew）。

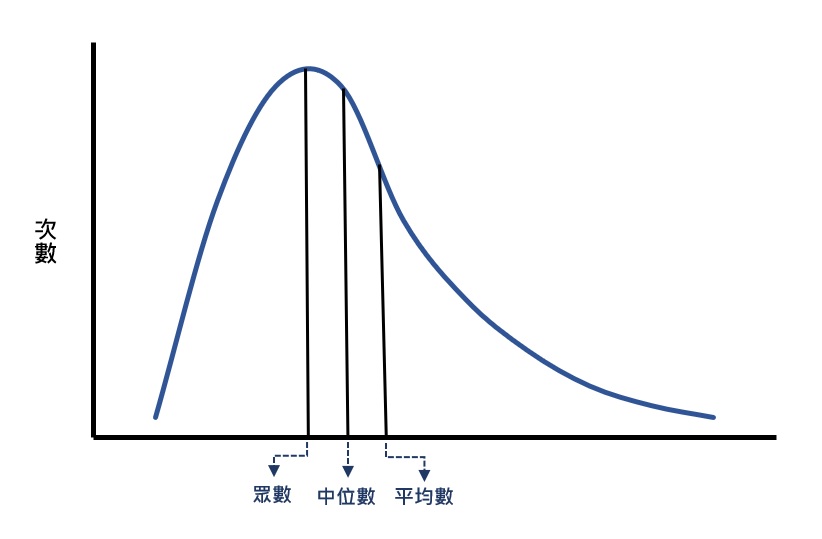
若大多數的數值集中在低分的一側，且另一側尾端的次數隨著數值的提升而慢慢地減少，稱為正偏態。由此可見，正偏態裡會有分數較高的離群值或極端數值。由於平均數很容易受到極端數值的影響，所以在正偏態分配裡，平均數會靠近高分之一側，換句話說，會高於眾數和中位數，如下圖。

相反地，若大多數的數值集中在高分的一側，且另一側尾端的次數隨著數值的降低而慢慢地減少，則稱為負偏態。由此可知，負偏態裡會有分數較低的離群值或極端數值，造成平均數往低分之一側移動，使其低於眾數與中位數，如下圖。

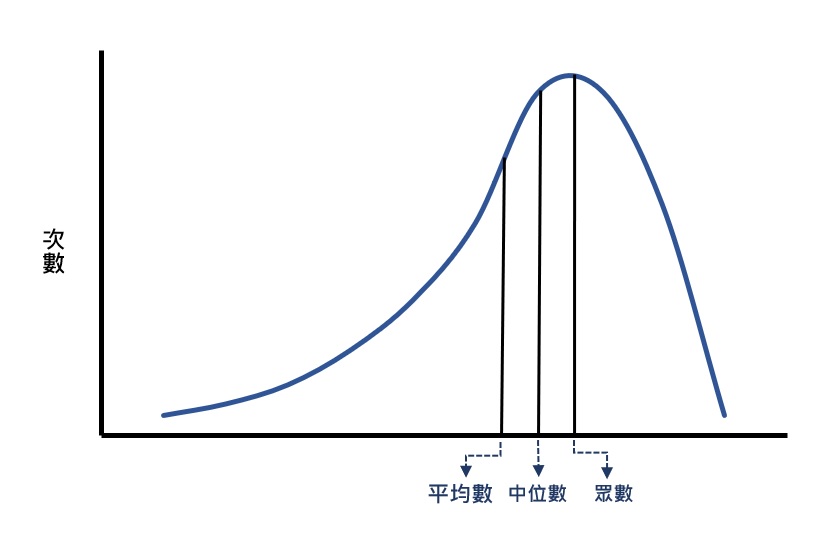
以上為本篇文章對於集中趨勢測量和偏態分配之間關係的介紹，希望透過本篇文章，您瞭解了數值的分布型態如何影響眾數、中位數和平均數這3個集中趨勢測量的相對位置。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站喔！另外，也歡迎您按讚和追蹤我們的Facebook和Twitter專頁喲！