如何使用Excel製作Q-Q plot

Q-Q plot是一種資料檢視的圖形工具，可用來評估一組樣本資料是否符合某種特定的機率分配形狀，最常用在常態分配上。雖然資料檢視的方法有很多種，例如次數分配、分組分數次數分配、直方圖、盒形圖，但實際運用機率分配數值的Q-Q plot可說是一種更好的方法。

利用統計分析軟體如SPSS可以很簡單地製作出Q-Q plot，不過若沒有專門的統計分析軟體，運用微軟的Excel也可以繪製出相同的圖形。雖然繪製過程須使用到函數且操作步驟較多，但圖形的調整選項很多，完成後的外形也很美觀。

下面內容將直接示範如何使用Excel製作Q-Q plot，不做定義或概念等學理內容的介紹。若您想瞭解這圖形的使用時機和製作概念，請參考Q-Q plot使用時機和運用SPSS製作的方法。

• 如何使用Excel製作Q-Q plot
  1. 資料轉換成標準化的分數
  2. 標準化的分數從小至大排序
  3. 利用等級計算分數的百分等級
  4. 常態曲線下標準分數的尋找
  5. 製作Q-Q plot

如何使用Excel製作Q-Q plot

為了示範過程的方便，這裡僅使用10個分數作為資料，並藉由Q-Q plot的製作來檢視這10個分數是否為常態分配。您可以使用自己的資料來繪製，若您的資料為SPSS檔案格式，須先將資料匯出至Excel後才能進行操作。如果想瞭解SPSS資料檔匯出至Excel的方法，請參考匯出SPSS資料至Excel並繪製盒形圖。

先開啟一空白的工作表，以一欄為一個變項的資料且第1列為變項名稱的方式，將資料輸入至工作表裡。若是從SPSS匯入資料，則維持原本的資料形式即可。這裡使用的資料有2個變項，分別為樣本編號（ID）和分數（SCORE），下面將逐步示範Q-Q plot的製作方法。

1. 資料轉換成標準化的分數

Q-Q plot不一定要使用標準化的分數來製作，若想要維持資料原本的測量單位也沒有問題。不過習慣上，X座標軸和Y座標軸通常為相同的單位，且為了讓圖形簡明易懂，所以這裡仍將資料轉換成平均數為0、標準差為1的標準分數。

把資料轉換成標準化分數的函數為STANDARDIZE，而這個函數的語法為STANDARDIZE(x, mean, standard_dev)，括弧裡3個引數分別代表欲轉換的分數、所有分數的平均數和所有分數的標準差。由於這函數須使用到平均數和標準差，所以要再利用AVERAGE和STDEV.S兩個函數。

平均數AVERAGE函數的語法為AVERAGE(number1, [number2], …)，而標準差STDEV.S函數的語法為STDEV.S(number1, [number2], …)，兩者在括弧裡的引數皆指資料的範圍。這2個函數可巢套在STANDARDIZE函數裡第2和第3個引數的位置。

在SCORE右邊欄的第1個儲存格（C1）輸入ZSCORE，代表資料標準化後的分數，然後在下方的儲存格C2輸入下面的語法：

=STANDARDIZE(B2, AVERAGE($B$2:$B$11), STDEV.S($B$2:$B$11))

這語法指出先計算出位於儲存格B2到B11的10個分數之平均數和標準差，再計算位在儲存格B2的分數之標準化分數。這裡在表示儲存格位置的英文字母（欄）和阿拉伯數字（列）前分別加上一個金錢符號（$）的方法，代表把儲存格固定在這個位置，當函數語法被複製到其他的儲存格時，原本參照的儲存格位置不會因此改變，稱為「絕對參照」（absolute references）。

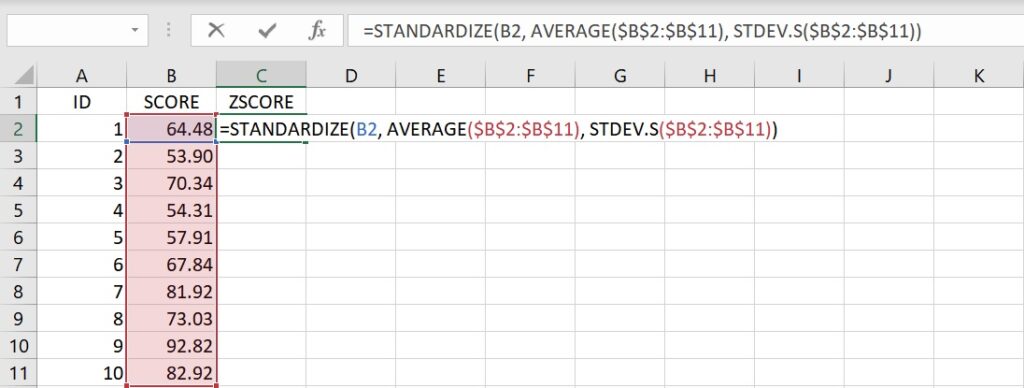
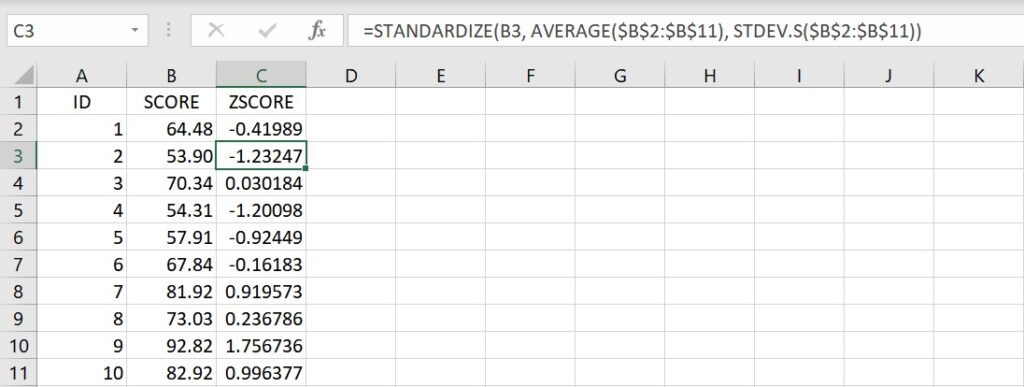
複製儲存格C2的語法並貼上到儲存格C3至C11裡，就可得到所有分數的標準化分數。透過「絕對參照」的方式，可發現在STANDARDIZE函數語法裡，只有第1個引數（欲轉換的分數）隨著儲存格的移動而產生變化，第2和第3個引數都不會改變。例如下圖裡儲存格C3的語法，只有第1個引數變成B3，其他引數都沒改變。

2. 標準化的分數從小至大排序

計算出每一個分數的標準化分數後，接下來把位於C欄的標準化分數從小至大排序。您也可以選擇排序B欄的原始分數，並不會影響排序的結果。

分數排序可以透過RANK.AVG函數來達成，這函數的語法為RANK.AVG(number, ref, [order])，括弧裡第1個引數指欲排序的分數，第2個引數為欲排序的資料範圍，第3個引數指排序的方法。第3個引數不是必要的引數，所以包覆在方括弧裡，若省略不寫或填入數字0，為從大至小排序；若填入數字1，則為從小至大排序。如果資料裡存在相同等級，這函數會傳回平均等級。

在ZSCORE右邊欄的第1個儲存格（D1）輸入RANK，代表分數的等級，然後在RANK下方的儲存格D2輸入下面的語法：

=RANK.AVG(C2, $C$2:$C$11, 1)

這語法指出把位於儲存格C2到C11的資料進行從小至大的排序，並傳回位於儲存格C2的分數之等級。這裡同樣運用「絕對參照」的方式，把資料範圍固定在儲存格C2到C11間，以利之後的複製與貼上操作。

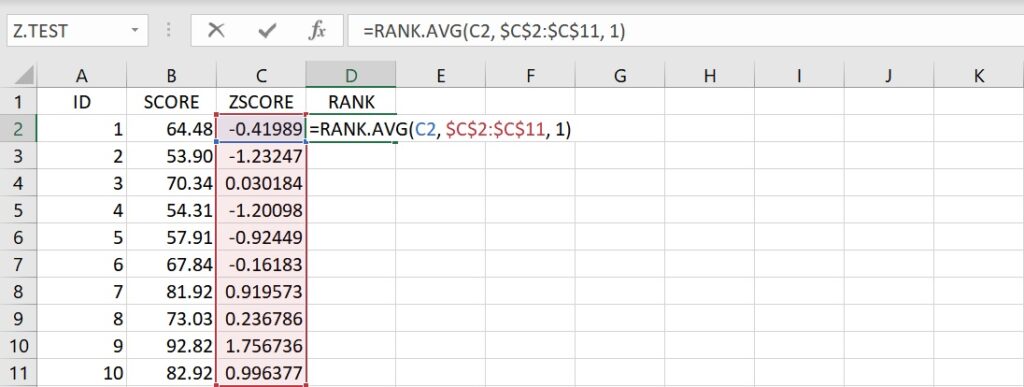
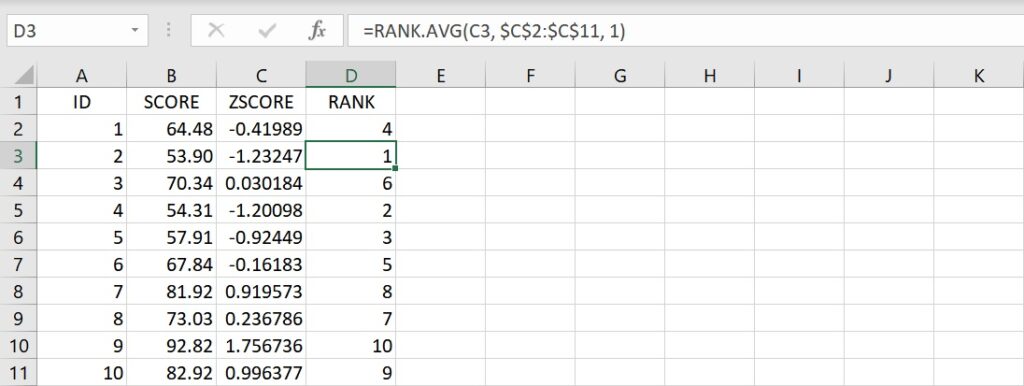
複製儲存格D2的語法並貼上至儲存格D3到D11裡，即可得到各個標準化的分數從小到大排序後的等級。同樣地，因為使用「絕對參照」的方法，所以語法貼上到不同儲存格的時候，只有第1個引數（欲排序的分數）隨著儲存格的移動而改變。

3. 利用等級計算分數的百分等級

計算百分等級的方法有很多種，這裡採用廣泛被使用且方法折衷的Hazen公式來計算（2013）。若讓代表一個分數的等級，為分數的總個數，Hazen公式如下：

   

上面的公式須使用到分數的總個數，若樣本數很少，當然可以直接數出來，但當樣本數很大的時候，就要透過函數來計算。COUNT函數能夠數出帶有數字的儲存格數目，語法為COUNT(value1, [value2], …)，括弧裡的引數指欲計算出總數的儲存格範圍。

在RANK右邊欄的第1個儲存格（E1）輸入PR，代表分數的百分等級，然後在PR下方的儲存格E2輸入下面的公式：

=(D2-0.5)/COUNT($D$2:$D$11)

這公式即是上面的Hazen公式，把一個分數的等級減去0.5後再除以分數的總個數。由於這裡要以比例而不是百分比的方式呈現，所以沒有乘以100。同樣地，這裡使用「絕對參照」的方式，將COUNT函數的資料範圍固定在儲存格D2和D11間。

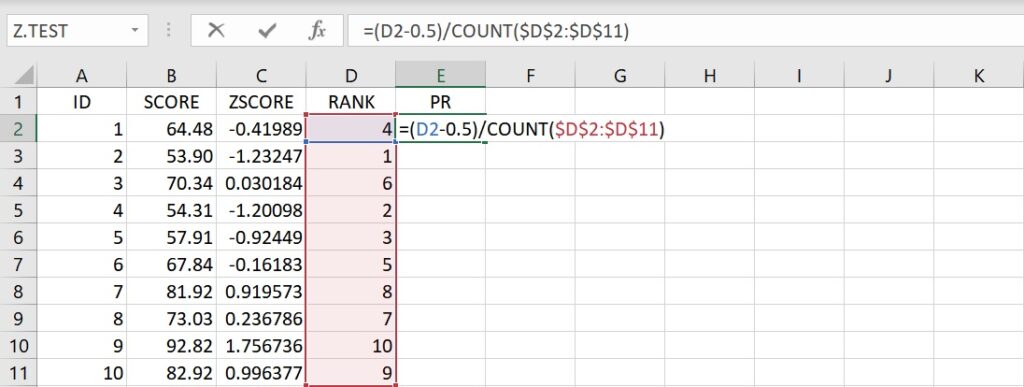
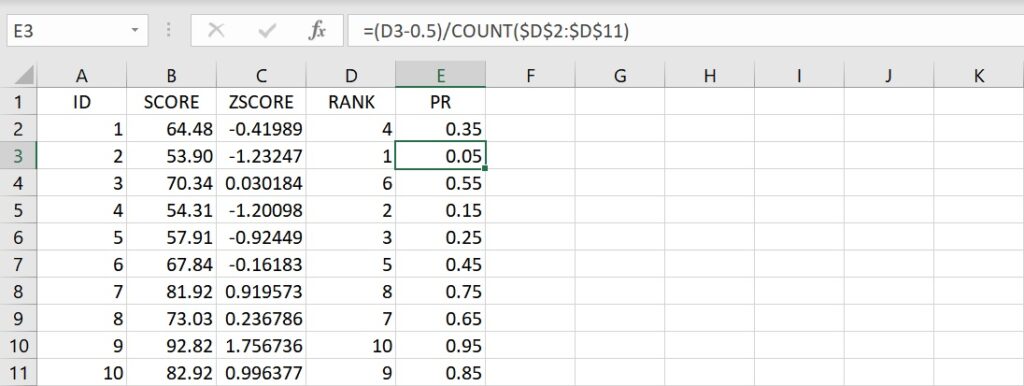
複製儲存格E2的公式並貼上至儲存格E3到E11裡，就可得到每個分數的百分等級。例如第1個分數的百分等級為0.35，這數值顯示有35%的分數落在這個分數的下面（也就是小於這個分數），其他的百分等級也都可以做這樣的解釋。

4. 常態曲線下標準分數的尋找

計算出各個分數的百分等級後，要尋找在常態曲線下相同等級所對應的標準分數，換句話說，要從常態曲線下面積去尋找標準分數。利用Excel尋找常態曲線下面積或分數的詳細介紹，請參考如何使用Excel尋找常態曲線下面積或分數。

這裡要利用NORM.S.INV函數，語法為NORM.S.INV(probability)，括弧裡的引數指常態分配的機率，在這裡就是每個分數的百分等級。

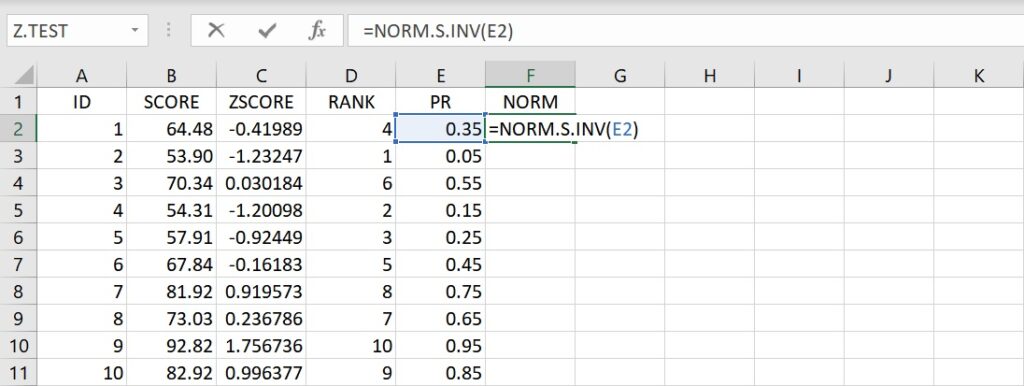
在PR右邊欄的第1個儲存格（F1）輸入NORM，代表常態曲線下的標準分數，並在NORM下方的儲存格F2輸入下面的語法：

=NORM.S.INV(E2)

這語法要求NORM.S.INV函數尋找常態曲線下的面積（也可說是機率）為0.35時的標準分數，會傳回數值-0.38532。這數值指出，當分數的百分等級為0.35時，常態分配曲線下相對應的標準分數為-0.38532。

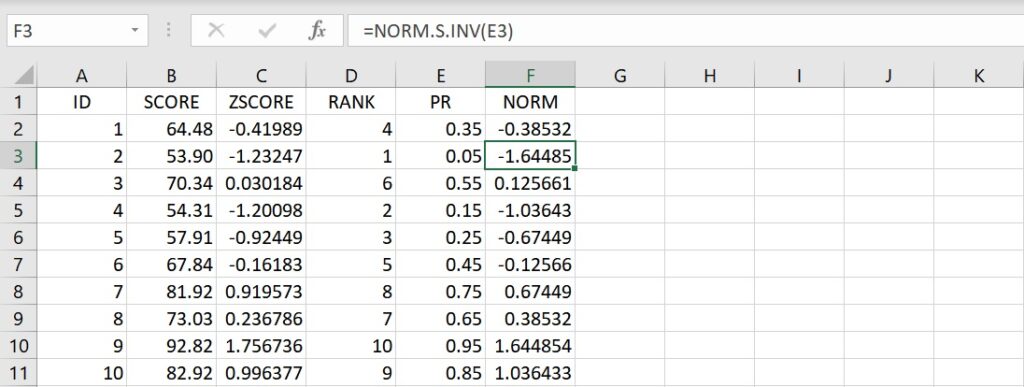
複製儲存格F2的語法並貼上至儲存格F3到F11裡，傳回的數值就是與各個分數的百分等級相對應的常態曲線下的標準分數。

5. 製作Q-Q plot

完成上述的4個步驟後，就可開始製作Q-Q plot。先用滑鼠選取C欄ZSCORE下方的所有數值，按住鍵盤的ctrl鍵再用滑鼠選取F欄NORM下方的所有數值，然後點選功能表的插入 » 圖表 » 插入XY散佈圖或泡泡圖 » 散佈圖。

透過功能表單的選擇，會出現如下的圖形，即為Q-Q plot。不過這圖形不太符合一般常見的Q-Q plot，所以須做一些外觀上的調整。

先用滑鼠在Q-Q plot的任何一處點一下，再點選功能表的圖表設計 » 圖表版面配置 » 新增圖表項目，下拉選單中有許多圖形調整的選項，例如座標軸、座標軸標題、圖表標題、資料標籤、格線、趨勢線等，可依據個人的需要或喜好進行相關的調整。

在刪除圖表標題、新增X和Y座標軸標題、刪除所有格線和新增一條線性趨勢線後，Q-Q plot變成下圖的樣子。

若要調整座標軸的格式，例如座標軸的範圍、X和Y座標軸交叉的地方、座標軸線條的粗細和顏色等，可在欲調整的座標軸上用滑鼠點一下，再點選功能表的格式 » 目前的選取範圍 » 格式化選取範圍，會帶出座標軸格式的工作窗格，從這裡能夠進行任何與座標軸相關的調整。

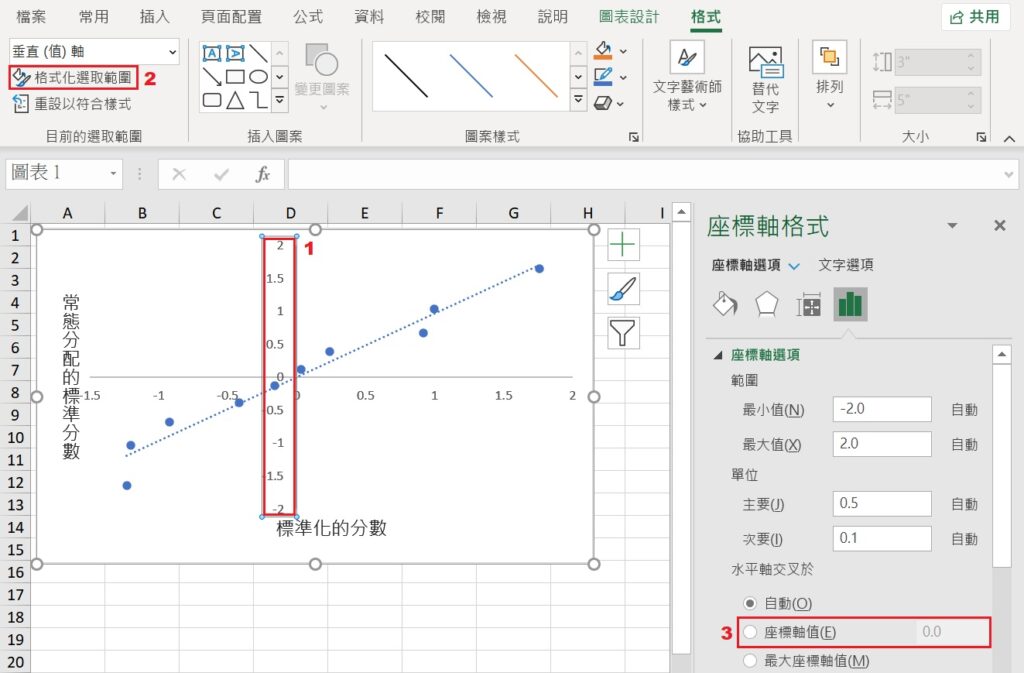
經過X座標軸最小值的調整、兩座標軸主要單位的更改、兩座標軸交叉位置的調整後，Q-Q plot變成下圖的樣子。

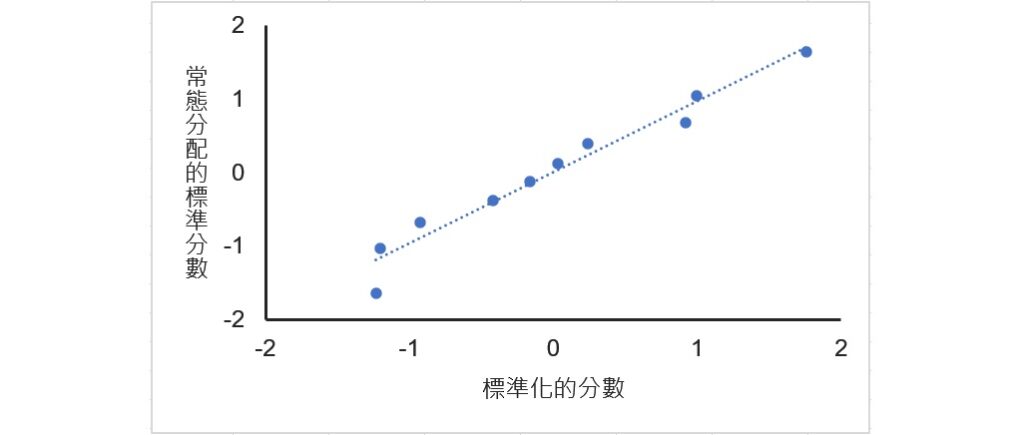
最後，若要調整圖形裡面資料圓點的外觀，例如不要填滿顏色、外框顏色的改變、圓點大小的調整等，可用滑鼠在圖形上的任何一個圓點上點一下，再點選功能表的格式 » 目前的選取範圍 » 格式化選取範圍，會帶出資料數列格式的工作窗格，從這裡能夠進行任何與資料數列相關的調整。若想改變趨勢線的外觀，也可透過相同的步驟來變更。

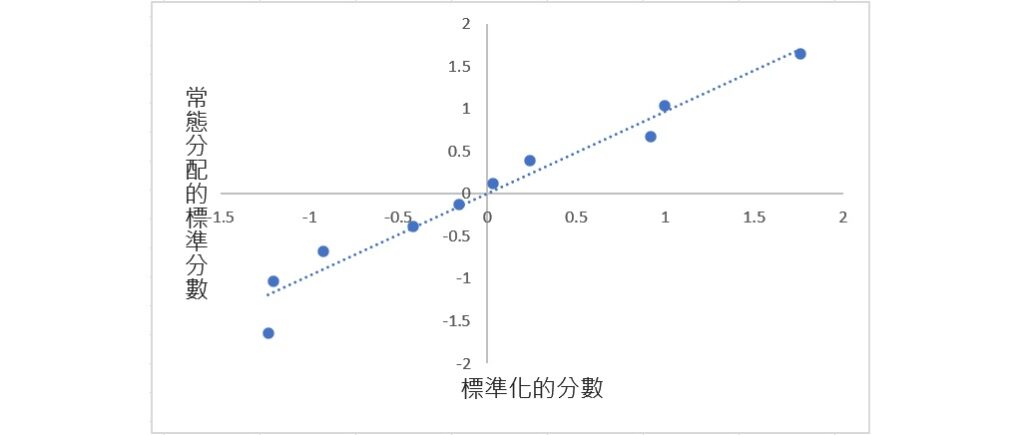
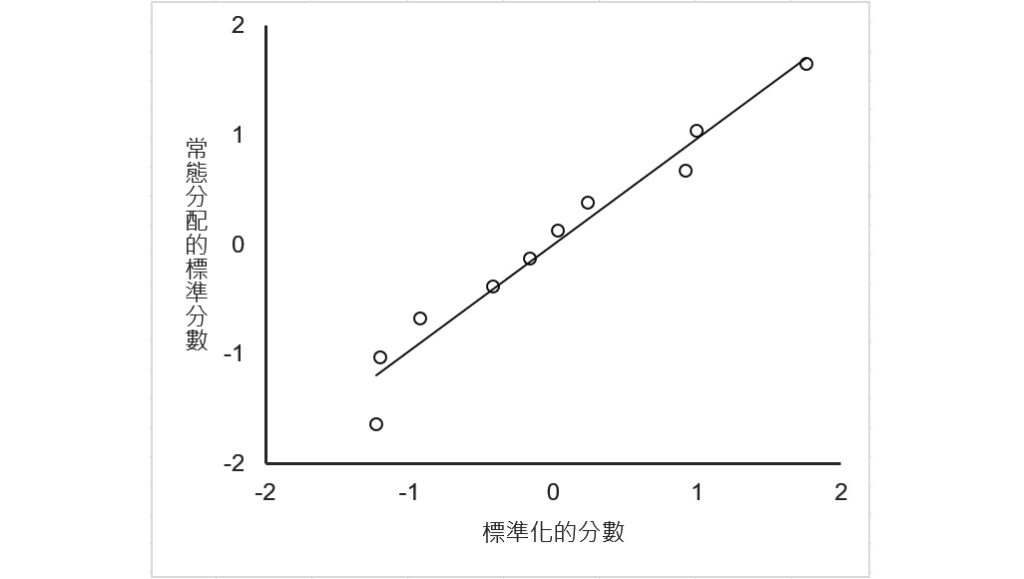
經過資料圓點和趨勢線外觀的調整後，再修正一下整個圖形的長寬比率，最後完成的Q-Q plot如下圖。從下圖可以看出，這10個分數大多落在或很靠近45度角的直線，並沒有大幅度地偏離，可說是常態分配。

從上面的示範過程可以發現，利用Excel能夠製作出Q-Q plot，雖然過程中須使用到函數來進行一些計算，但圖形外觀調整的選項很多，完成後的圖形也很美觀。若您沒有統計分析軟體，但須要繪製Q-Q plot時，不妨試試上面介紹的方法喔！

以上為本篇文章對如何使用Excel製作Q-Q plot的介紹，希望透過本篇文章，您學會了函數的使用以及Q-Q plot的製作方法。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習資源，並持續回訪本網站喔！另外，您也可以在Facebook和Twitter上找到我們喲！

參考資料

Bornmann, L., Leydesdorff, L., & Wang, J. (2013). Which percentile-based approach should be preferred for calculating normalized citation impact values? An empirical comparison of five approaches including a newly developed citation-rank approach (P100). Journal of Informetrics, 7(4), 933-944. https://doi.org/10.1016/j.joi.2013.09.003