平均數抽樣分配的定義和特性

抽樣分配（sampling distribution）是指從母群體中隨機抽取出樣本大小為 $N$ 的所有可能樣本，計算出每一個樣本的統計量與獲得該統計量的機率，並將各個統計量的機率分布狀況呈現出來的一種機率分配。每一種統計量都有抽樣分配，平均數抽樣分配就是其中的一種。

抽樣分配的功用類似於次數分配（frequency distribution），藉由次數分配可以看出分數整體的分布狀況和各個分數的百分等級，而透過抽樣分配可以看出樣本統計量的分布狀況和各個統計量的發生機率。兩者的差別在於次數分配是利用研究的原始數據所得到的實徵上（empirically）分配，抽樣分配則是利用樣本統計量所導出的理論上（theoretically）分配。

抽樣分配和推論統計息息相關，每一種統計檢定方式都有相應的抽樣分配，例如平均數抽樣分配、ｔ分配、卡方分配和Ｆ分配。假設檢定的過程中，在計算出合適的統計量（也就是檢定統計量）之後，會利用該檢定相應的抽樣分配來評估計算得到的統計量，藉此決定是否可拒絕虛無假設。換句話說，抽樣分配提供了一個比較統計結果的基準，使得一個統計量變得有意義。

本篇文章將介紹平均數抽樣分配，一種外觀趨近於常態分配的抽樣分配，用在單一樣本ｚ檢定的假設檢定上。以下將先介紹平均數抽樣分配的定義，再說明這種抽樣分配的特性。

平均數抽樣分配的定義
平均數抽樣分配的特性

平均數抽樣分配的定義

依據抽樣分配的概念，平均數抽樣分配（sampling distribution of the mean）的定義為從母群體中隨機抽取出樣本大小為 $N$ 的所有可能樣本，計算出每一個樣本的平均數和獲得該平均數的機率，並呈現出各個平均數的機率分布狀況。

理論上的定義可能讓您一頭霧水，這裡用個簡單的例子來說明平均數抽樣分配。假設有一個母群體，裡面有5個分數（實際上母群體不可能這麼小，此處只是為了便於理解，才將母群體限縮為5個數值），分別為1、3、5、7、9，平均數為5，標準差為2.828。

提醒：本文中所計算的標準差，不論是母群體標準差或下面提到的標準誤，因為皆牽涉到母群體本身，所以計算時，分母為 $N$ ，而不是樣本的 $N-1$ 。

若要從母群體的這5個分數導出樣本大小為2的平均數抽樣分配，步驟如下：

1. 列出樣本大小為2的所有可能樣本

從母群體的5個分數中，使用取出後再置回的方式，列出樣本大小為2的所有可能的樣本，如下表的「樣本分數組成」欄所示，總共可列出25組樣本。

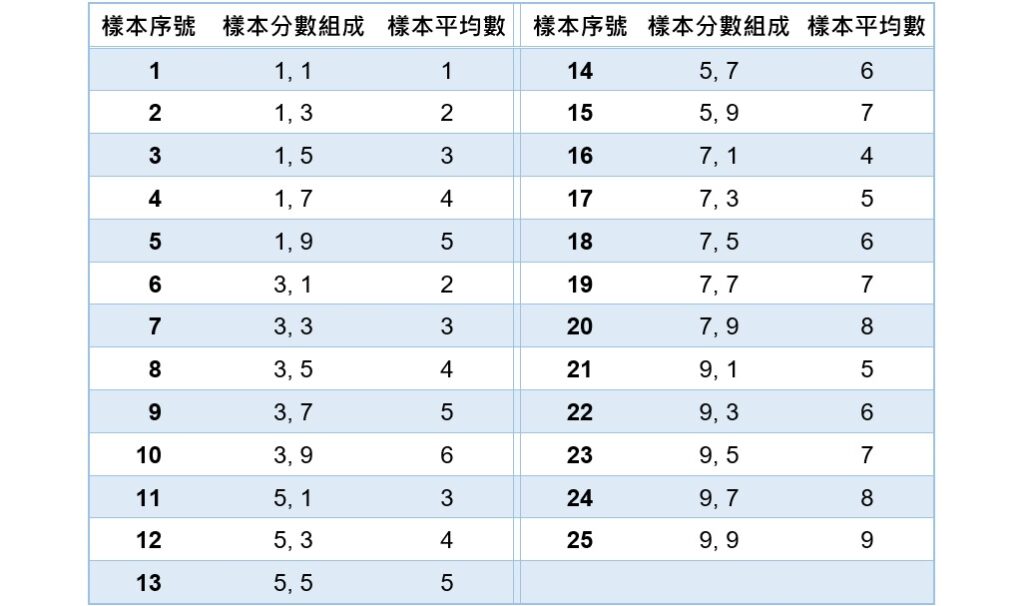
all possible samples of size 2 for sampling distribution of the mean

2. 計算出每一組樣本的平均數

因為這裡要導出平均數的抽樣分配，所以須計算出每一組樣本的平均數，如上表的「樣本平均數」欄所示。從上表可以發現，有些樣本的平均數和母群體平均數相同，有些則不同，此乃抽樣變異（sampling variation）所導致。由於每個樣本皆由不同的數值所組成，所以會產生和母群體平均數不同的結果。

3. 計算出獲得各個不同平均數的機率

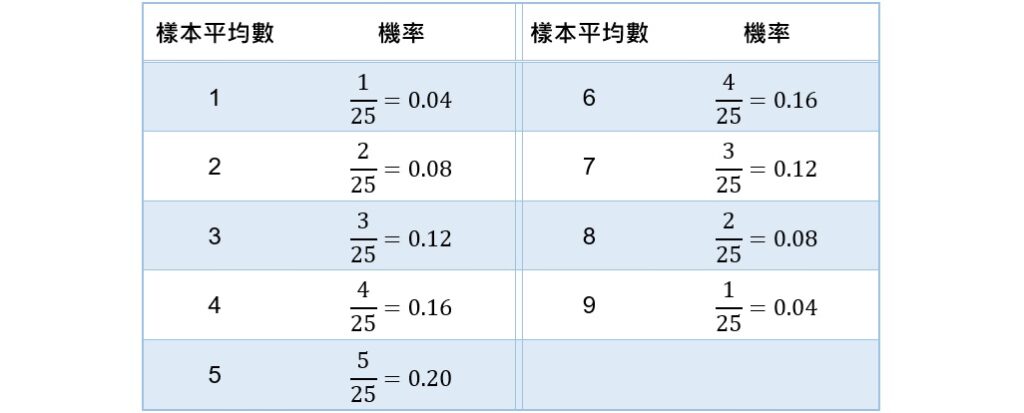
在25組的樣本中，平均數為1的只有1組，所以獲得平均數為1的機率為 $1 \div 25=0.04$ ；平均數為2的有2組，所以獲得平均數為2的機率為 $2 \div 25=0.08$ ，以此類推，計算出得到各個不同平均數的機率。下表即為獲得不同樣本平均數的機率，而這就是樣本大小為2的平均數抽樣分配。

probability of each mean for sampling distribution of the mean

為了瞭解樣本大小為2的平均數抽樣分配的形狀，可將樣本平均數置於橫座標軸、機率置於縱座標軸，繪製出下面的直方圖。

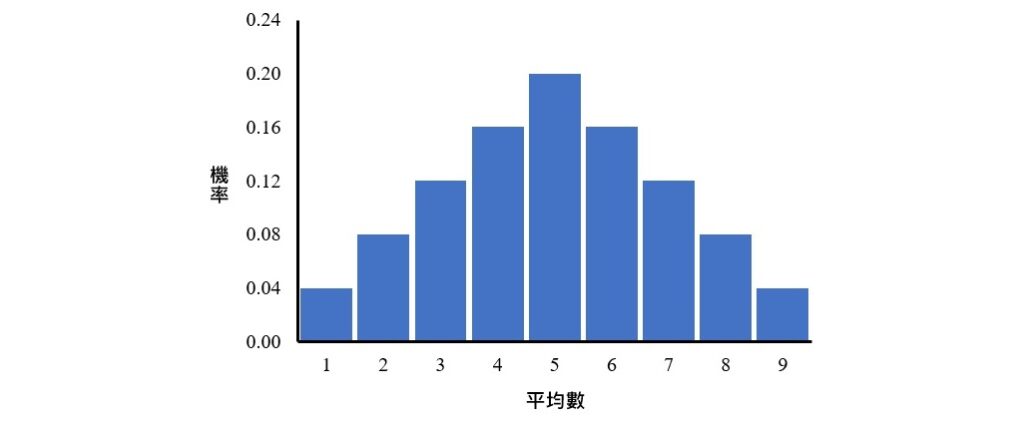
plot of sampling distribution of the mean when sample size equals 2

從上圖可看出，即使母群體沒有呈現常態分配（這裡的母群體只有1、3、5、7、9五個分數），而且樣本大小僅為2的情況下，平均數抽樣分配已呈現出常態分配的形狀。更多次數分配形狀的介紹，可以參考次數分配的形狀：常態、偏態和峰態。

因此，不管母群體是否呈現常態分配，當樣本數愈大的時候，平均數抽樣分配會愈趨近於常態分配，這就是所謂的中央極限定理（central limit theorem）。原則上，當 $N \ge 30$ 時，平均數抽樣分配已呈現常態分配；但當 $N<30$ 時，平均數抽樣分配並非為常態分配，此時為另一種分配型態，稱為ｔ抽樣分配。

平均數抽樣分配的特性

從上面的說明可以知道，平均數抽樣分配是從母群體隨機抽取出樣本大小為 $N$ 的所有可能樣本後，計算出每一個樣本的平均數與各個平均數的出現機率而來的機率分配。這個母群體本身有一個平均數和一個標準差，符號分別為 $\mu$ 和 $\sigma$ 。

若將每個樣本的平均數皆視為一個分數，則全部的樣本會有一個平均數，該平均數稱為平均數抽樣分配的平均數，符號為 $\mu_{\overline X}$ 。同樣地，全部的樣本也會有一個標準差，稱為平均數抽樣分配的標準差，即為常聽到的平均數標準誤（standard error of the mean），簡稱為標準誤（standard error），符號為 $\sigma_{\overline X}$ 。

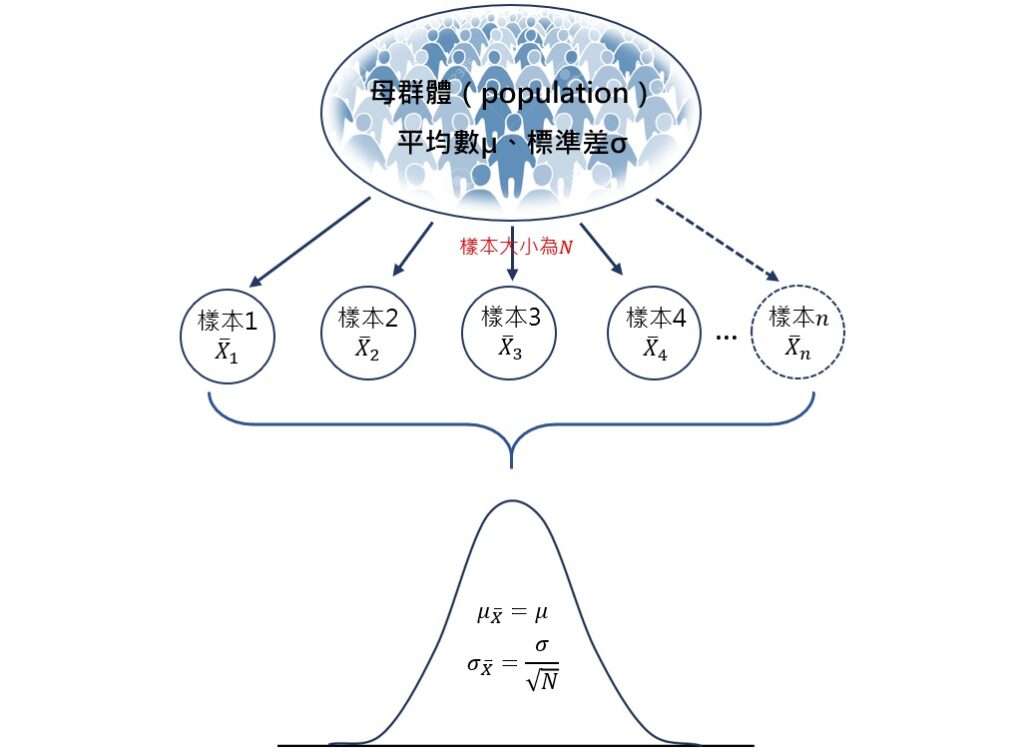
generation of sampling distribution of mean

不論產生抽樣分配的樣本大小為何，平均數抽樣分配的平均數和標準差都具有2個重要的特性：

平均數抽樣分配的平均數等於母群體的平均數， $\mu_{\overline X}=\mu$ 。
平均數抽樣分配的標準差（標準誤）等於母群體標準差除以 $\sqrt N$ ， $\displaystyle \sigma_{\overline X}=\frac {\sigma}{\sqrt N}$ 。

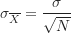我們可利用上面所舉的例子來驗證上述的2個特性。假設母群體有1、3、5、7、9五個分數，從這個母群體中隨機抽取樣本大小為2的樣本，取出後置回，共可抽取出25組樣本。將每一組樣本的平均數視為一個數值（下表的「樣本平均數 $\overline X_i$ 」欄），則所有數值的平均數為：

$\mu_{\overline X}=\frac {125}{25}=5$

計算結果得到平均數抽樣分配的平均數為5，和母群體的平均數相同，證實 $\mu_{\overline X}=\mu$ 。

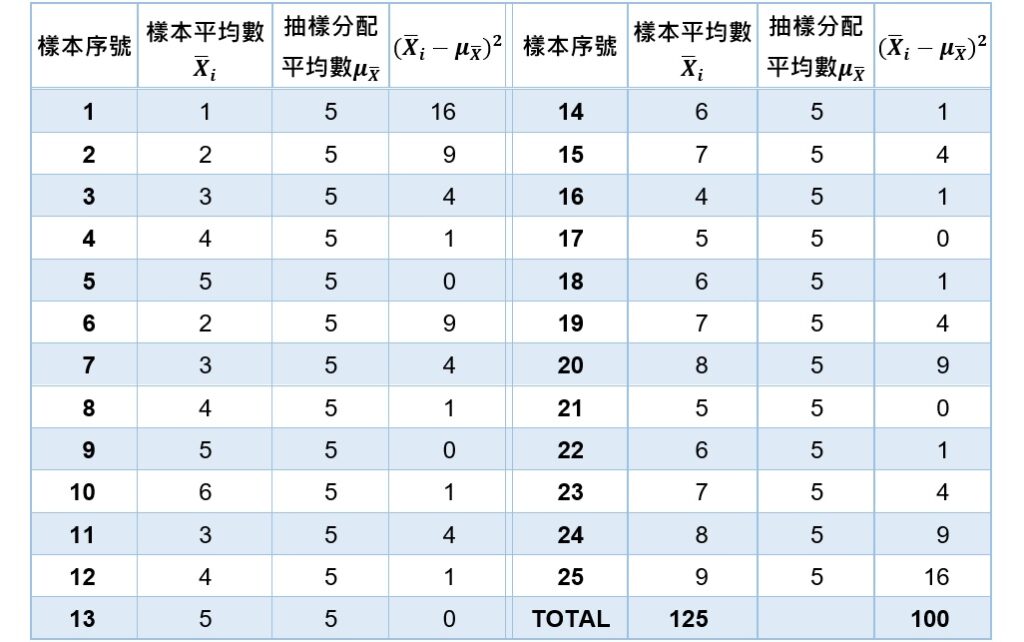
computation of mean and standard error for sampling distribution of the mean

接著，利用上表的離差平方和 $(\overline X_i-\mu_{\overline X})^2$ 欄，計算這25個數值的標準差：

$\begin{equation*}\begin{align}\sigma_{\overline X}&=\sqrt {\frac {\sum_{i=1}^n (\overline X_i-\mu_{\overline X})^2}{25}} \\&=\sqrt {\frac {100}{25}} \\&=\sqrt 4 \\&=2\end{align}\end{equation*}$

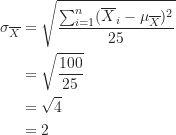
結果顯示平均數抽樣分配的標準差（標準誤）為2。將母群體的標準差 $\sigma$ 除以 $\sqrt {N}$ ， $\displaystyle \frac {2.828}{\sqrt {2}}= 2$ ，證實了 $\displaystyle \sigma_{\overline X}=\frac {\sigma}{\sqrt N}$ 。

總結來說，不管樣本數 $N$ 的大小，平均數抽樣分配的特性有以下3點：

$\boldsymbol {\mu_{\overline X}=\mu}$ ：平均數抽樣分配的平均數和母群體平均數相同。
$\boldsymbol {\sigma_{\overline X}=\dfrac {\sigma}{\sqrt N}}$ ：平均數抽樣分配的標準差，也就是標準誤，等於母群體的標準差除以 $\sqrt N$ 。
中央極限定理：即使母群體本身沒有呈現常態分配，但當樣本數愈大的時候，平均數抽樣分配會愈趨近於常態分配。

雖然此處討論的抽樣分配為平均數抽樣分配，但這裡所提及的概念皆可適用到其他類型的抽樣分配。如同文章一開始所提，每一統計檢定方式皆有相應的抽樣分配，在假設檢定的過程中，才可評估由樣本資料計算出來的檢定統計量，進而決定拒絕或保留虛無假設。

以上為本篇文章對平均數抽樣分配的介紹，希望透過本篇文章，您瞭解了抽樣分配的意義、平均數抽樣分配的定義和特性。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習資源，並持續回訪本網站喔！另外，您也可以在Facebook和Twitter上找到我們喲！

平均數抽樣分配的定義

1. 列出樣本大小為2的所有可能樣本

2. 計算出每一組樣本的平均數

3. 計算出獲得各個不同平均數的機率

平均數抽樣分配的特性

您可能也會喜歡