集中趨勢的測量

整理數據資料時，雖然使用次數分配表（參考次數分配的意義和分組分數次數分配的文章）或圖形能夠看出資料整體的分布情形，但卻沒有一個量化的數值可以描述整體分配的狀態，也無法在兩個以上的分配間進行量化的比較。

舉例來說，一位老師想要比較A班和B班的統計學期末考成績，在製作了次數分配表和繪製了圖形後，雖然大略可看出分數的分布情形，但仍舊無法看出哪一班的成績較好，此時就需要一個可代表班級成績的量化數值。通常在此種情況，會計算出各班的平均成績，然後再進行比較，而「平均成績」即為一個分配的集中趨勢（central tendency）。

最常被用來當作集中趨勢測量的數值有三種，分別為眾數（mode）、中位數（median）和平均數（mean），本篇文章將介紹這3種測量方式，再示範使用SPSS和Excel取得這3種統計量的方法。若您只對某一部分的內容感興趣，也可點選下面的連結，即可直接跳至您想閱讀的內容。

• 眾數
• 中位數
• 平均數
• 運用SPSS取得集中趨勢的統計量
• 運用Excel計算集中趨勢的統計量

眾數

眾數是指資料裡出現頻率最高的數值，為3種測量方式裡最簡單的一種。若有次數分配表，可藉由檢視次數的欄位，找到出現頻率最高的數值；若資料不多，也可透過紙筆運算的方式，將數值從小到大排列，記下每一個數值出現的次數，而出現最多次的數值即為眾數。

理想的狀態下，一個分配裡只有一個眾數，稱為單峰（unimodal）。但現實生活中，一個分配裡經常包含兩個以上的眾數，帶有兩個眾數的分配稱為雙峰（bimodal），而超過兩個眾數的分配則稱為多峰（multimodal）。下面3張圖即為不同的眾數分配形狀之例子。

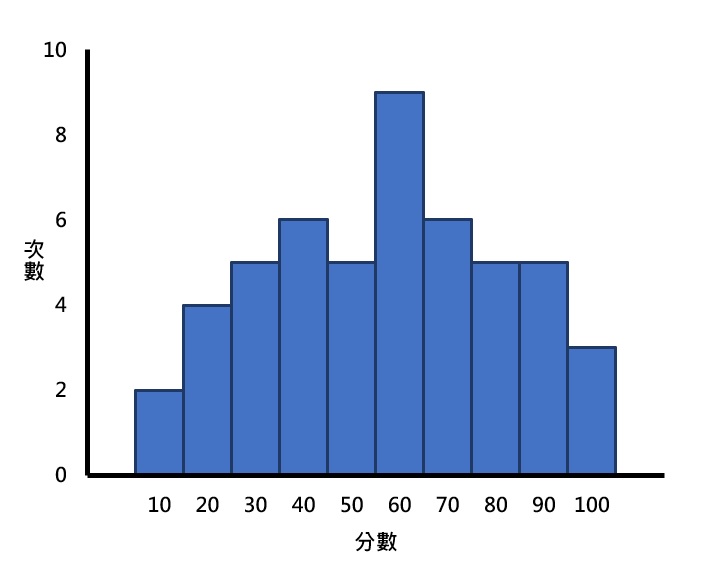
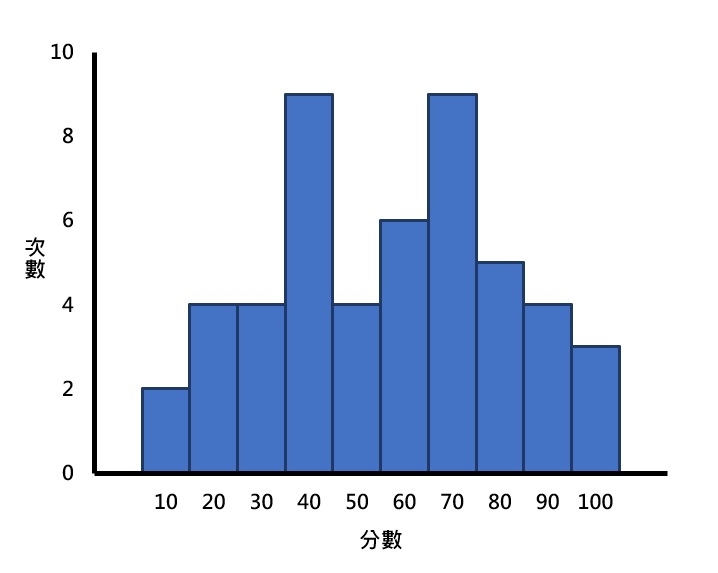
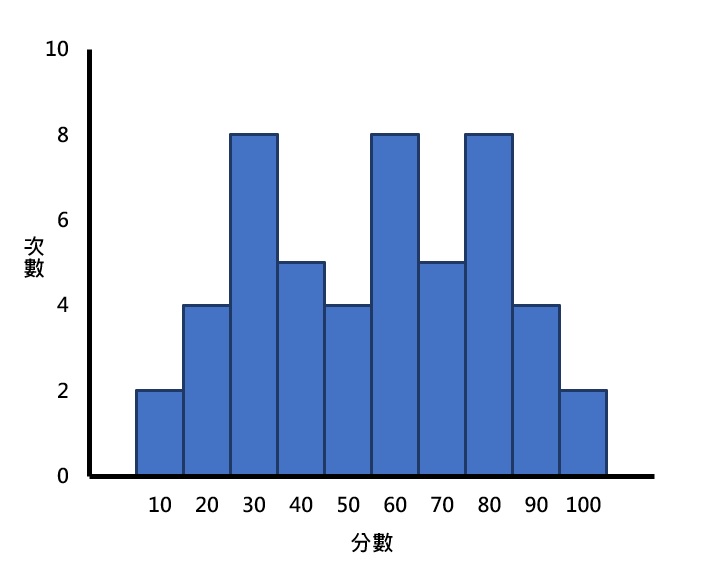
眾數可以使用在名義、次序、等距和比率等所有測量尺度的變項資料上，若想更深入瞭解測量尺度，可以閱讀測量尺度的意義和分類。雖然眾數是集中趨勢裡最簡單的一種測量方式，但一個分配裡通常不會只有一個眾數，而且眾數並沒有考量到分配裡的其他數值，僅以出現次數最多的數值為準，因此並沒有很常被使用。

中位數

第2個集中趨勢測量的數值是中位數，也稱為中數。中位數是指數值從小至大排序後最中間的數值，也就是第50百分位數，代表有50%的數值落在中位數之下。有關百分位數的概念，可以參考累積百分比曲線圖的繪製與用途之文章。

計算中位數時，須分成「原始數據的總個數為奇數」和「原始數據的總個數為偶數」等兩種情況。將原始數據從小至大排列後，若總個數為奇數，中位數為最中間的數值；若總個數為偶數，中位數則為最中間兩個數值的平均值。嘗試思考下面的兩個問題：

Q1：原始數據為56、20、77、45、18、22、68、92、101，中位數是多少？
數值從小至大排序：18、20、22、45、56、68、77、92、101
總共有9個數值，所以中位數是最中間的數值，也就是56。

Q2：原始數據為59、80、16、25、78、90、47、89，中位數是多少？
數值從小至大排序：16、25、47、59、78、80、89、90
總共有8個數值，所以中位數是最中間兩數值的平均值，也就是

因為中位數是最中間的數值，計算時並未將所有原始數據納入考量，所以相對地不容易受到極端數值或離群值的影響。此外，中位數也相對地不容易受到偏態分配的影響（關於偏態分配的介紹，可參考次數分配的形狀：常態、偏態和峰態），而且可使用在次序、等距和比率尺度的變項資料上，但無法使用在不具備數值次序特質的名義尺度變項資料上。

平均數

第3個集中趨勢的測量方法為平均數，也是一般人最耳熟能詳的數值，很常出現在新聞報導中，例如平均薪資、平均工作時數、平均房價等。平均數的計算方式是將所有的原始數據加起來後，再除以原始數據的總個數，可以用下面的公式呈現：

   

代表平均數，是總和的符號，代表第個成績，則是指數值的總個數。上述公式的分子即是加總所有的數值，分母則為數值的總個數。舉例而言，若原始數據有8個數值，16、25、47、59、78、80、89、90，其平均數的計算方式如下：

   

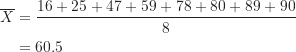
不像中位數，平均數很容易受到極端數值的影響，若原始數據裡有極端數值，平均數會朝著極端數值的方向移動。此點可透過下表來說明，三組分數裡的前4個數值都相同，只有最後一個數值不相同，且數值愈來愈大。因為三組分數的總個數都是5，所以中位數皆落在第3個數值，也就是12；但平均數則因為最後一個數值的不同而不一樣，當最後一個數值愈大，平均數也愈大。

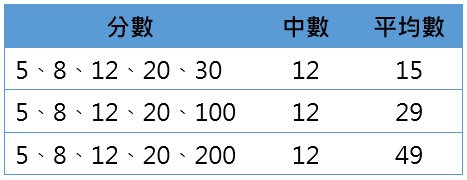
雖然平均數有易受極端數值影響的缺點，且只可用在等距和比率尺度的變項資料上，但仍舊是3種集中趨勢測量裡最常被使用的數值。主要的原因在於平均數使用了原始數據中的每一個數值，不像眾數、中位數僅依據少數幾個數值而決定，因此平均數較不易受到抽樣變異的影響，在不同的樣本間具有一定的穩定程度。

何謂抽樣變異（sampling variation）？
從一個母群體中隨機抽取數個樣本，每一個樣本都會有眾數、中位數和平均數3個數值。眾數和中位數會因為樣本的不同而有較大的變異，雖然平均數也會因為不同的樣本而有不同的數值，但與眾數和中位數相較，平均數的變異最小。平均數的此點特質相當重要，也是推論統計會使用平均數的主要原因。

集中趨勢的統計量可以很簡單地透過SPSS或Excel來計算，下面就來示範使用這2種軟體取得眾數、中位數和平均數的方式。

運用SPSS取得集中趨勢的統計量

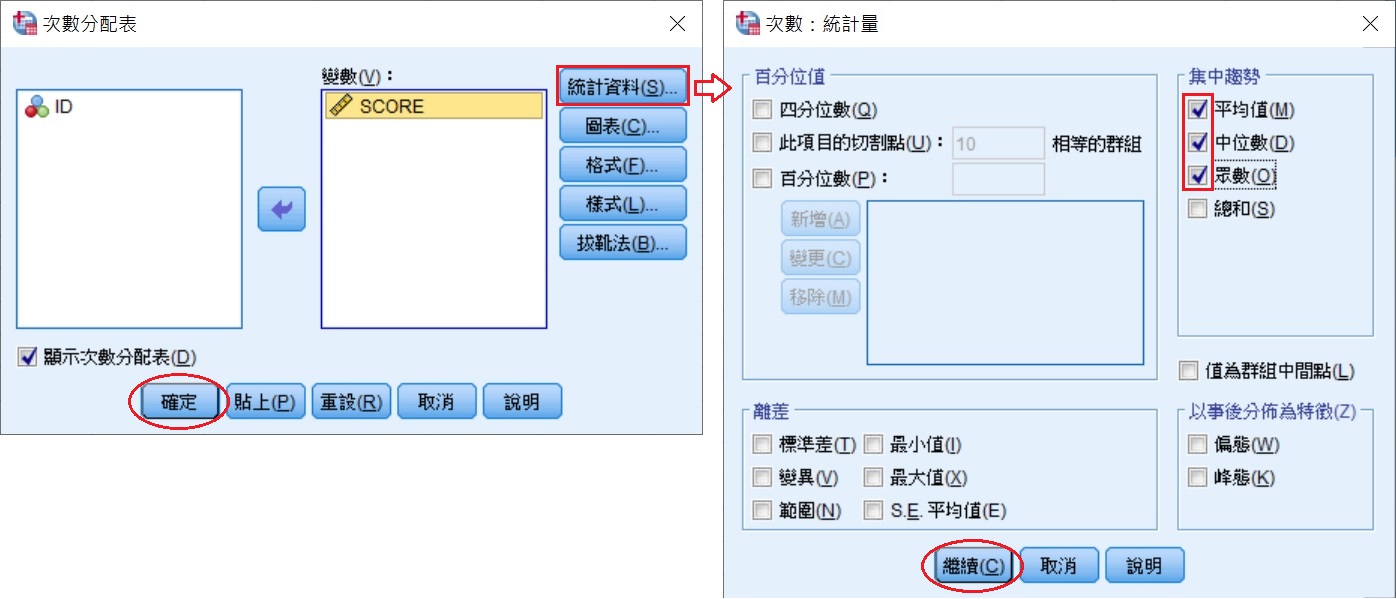
透過SPSS，可以很簡單地找到眾數、中位數和平均數。此處使用分組分數次數分配文章中50位學生的成績作為範例，點選SPSS資料編輯器功能表上的分析 » 敘述統計 » 次數分配表，帶出「次數分配表」視窗。關於SPSS資料輸入的方法，請參考SPSS操作環境和資料輸入。

將想要計算集中趨勢統計量的變項移至右邊的變數(V)方框中，接著按最右邊的統計資料(S)鈕，帶出「次數：統計量」視窗，勾選集中趨勢方框裡的平均值(M)、中位數(D)、眾數(O)之後，按下繼續(C)，回到「次數分配表」視窗後，再按下確定。

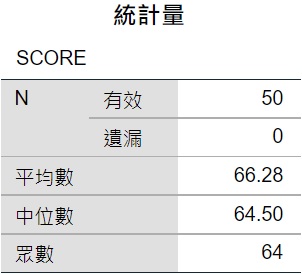
SPSS會輸出如下表的統計量，從這表格可以看出，50位學生成績的眾數為64分，中位數為64.5分，平均成績為66.28分。

從上面的過程可以發現，使用SPSS取得集中趨勢的3個統計量很簡單，只須用滑鼠點選圖形化的操作介面即可。但若要使用Excel，則須輸入函數來計算3個統計量，雖然比較麻煩，但操作上並不困難，以下就來看看。

運用Excel計算集中趨勢的統計量

將範例裡的50位學生成績輸入至Excel空白活頁簿裡，利用Excel計算集中趨勢的統計量須在儲存格裡輸入函數，眾數、中位數和平均數各自的函數和語法如下：

• 眾數：MODE.SNGL(number1,[number2],…)
• 中位數：MEDIAN(number1,[number2],…)
• 平均數：AVERAGE(number1,[number2],…)

三個函數的語法相同，括弧裡面直接輸入數值，每個數值間用逗點分開，也可以直接輸入數據資料的範圍。因為本範例有50個數值，逐一輸入太耗時，所以直接輸入資料的範圍B2:B51，計算眾數、中位數和平均數的函數和語法如下圖所示。

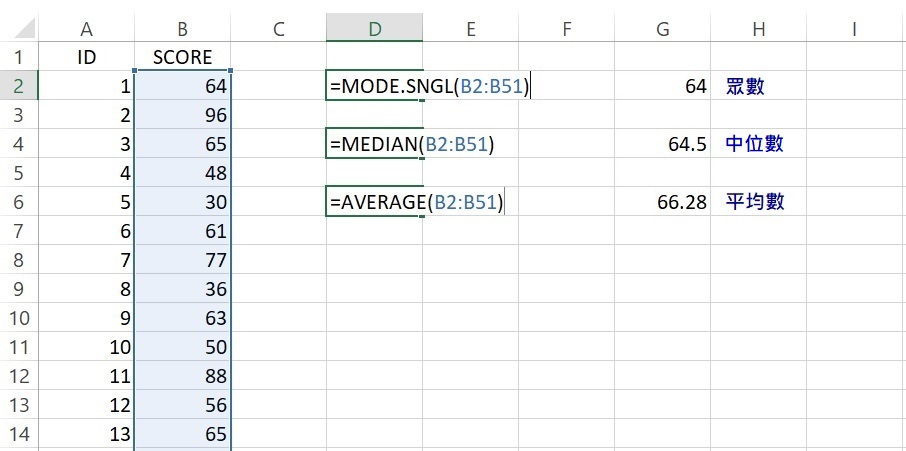
透過3個函數和語法的輸入，Excel輸出的眾數為64、中位數為64.5、平均數為66.28，與SPSS的輸出結果完全一致。

這裡要注意Excel的眾數函數，Excel 2010年後的版本將眾數函數分為MODE.SNGL和MODE.MULT兩個，若資料裡有多個眾數，使用MODE.SNGL函數只會輸出數值最小的那個眾數；若要輸出所有的眾數，則須使用MODE.MULT函數。

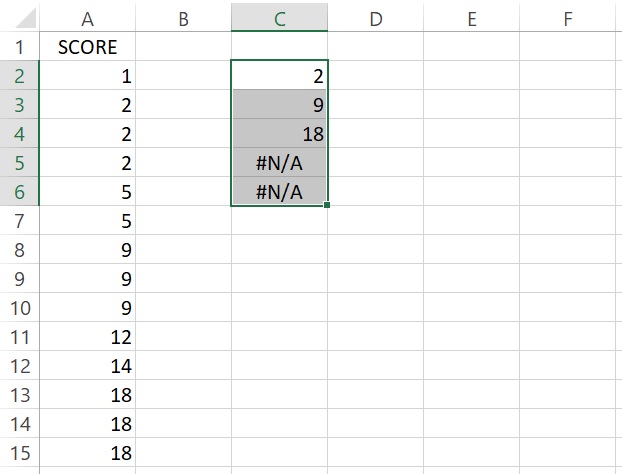
由於MODE.MULT函數會輸出多個結果，所以要使用陣列公式（array formula），操作上稍微不同於只輸出一個結果的函數。假設有14個數值，儲存格的範圍從A2到A15，如下圖。先選取輸出眾數的儲存格範圍，最好多圈選幾格，好讓所有的眾數都可被輸出，這裡選取C2到C6。

圈選完儲存格後，用鍵盤輸入=MODE.MULT(A2:A15)，再按Ctrl+Shift+Enter（若只按Enter，只會輸出數值最小的眾數），就會輸出資料裡所有的眾數。

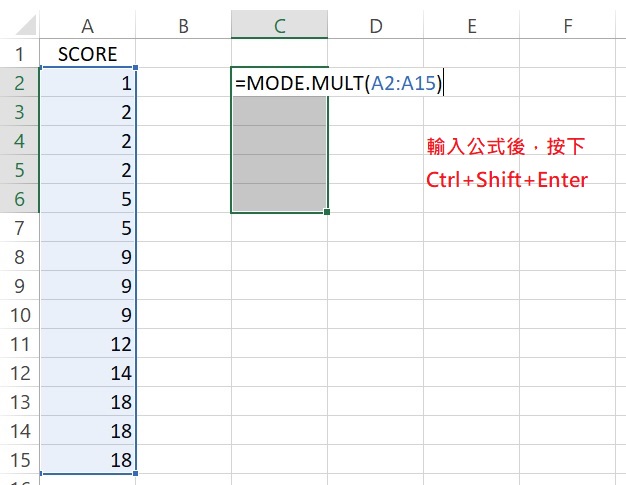
透過上面的步驟，Excel輸出2、9、18三個眾數值，多餘的輸出儲存格則會顯示「#N/A」的錯誤值，如下圖。

以上為本篇文章對集中趨勢測量的介紹，希望透過本篇文章，您瞭解了集中趨勢的3種測量方法，也學會使用SPSS和Excel取得集中趨勢的3個統計量。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站。此外，也歡迎您追蹤我們的Facebook和Twitter專頁喔！