🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
小樣本或σ未知的信賴區間之計算
信賴區間指可能包含母群體數值的一個數值範圍,不同於使用單一數值作為母群體參數估計值的點估計(point estimate),例如以樣本平均數![]() 作為母群體平均數
作為母群體平均數![]() 的估計值,信賴區間是使用一個範圍作為母群體參數的估計值,並指出母群體參數可能落在該區間的機率,屬於區間估計(interval estimate)。
的估計值,信賴區間是使用一個範圍作為母群體參數的估計值,並指出母群體參數可能落在該區間的機率,屬於區間估計(interval estimate)。
根據中央極限定理,當樣本數愈大時,抽樣分配會愈趨近於常態分配。因此,在信賴區間的意義和計算(σ已知)裡提到,當樣本數夠大且母群體標準差![]() 已知的時候,可以利用常態分配去尋找常態曲線下面積所對應的標準分數(z分數),進而計算出信賴區間。
已知的時候,可以利用常態分配去尋找常態曲線下面積所對應的標準分數(z分數),進而計算出信賴區間。
如果讓![]() 代表樣本平均數、
代表樣本平均數、![]() 為信賴區間的機率值(最常使用0.95或0.99)、
為信賴區間的機率值(最常使用0.95或0.99)、![]() 為母群體標準差、
為母群體標準差、![]() 為樣本總數,當樣本數目
為樣本總數,當樣本數目![]() 且母群體標準差
且母群體標準差![]() 已知時,信賴區間可用下面的不等式呈現:
已知時,信賴區間可用下面的不等式呈現:
![]()
然而,當無從得知母群體的標準差或樣本數較小時(![]() ),便無法使用上述的方式計算信賴區間,而須改用t分配(t distribution)來計算。以下將先介紹t分配的意義,再說明小樣本或
),便無法使用上述的方式計算信賴區間,而須改用t分配(t distribution)來計算。以下將先介紹t分配的意義,再說明小樣本或![]() 未知時信賴區間的計算方法,最後示範利用SPSS求得小樣本或
未知時信賴區間的計算方法,最後示範利用SPSS求得小樣本或![]() 未知時的信賴區間之操作過程。
未知時的信賴區間之操作過程。
t分配
t分配為抽樣分配的一種,由 William S. Gosset 於1908年提出。運用抽樣分配的概念,t分配是指從一母群體中隨機抽取出樣本大小為![]() 的所有可能樣本,計算出每一個樣本的t值與得到該t值的機率,最後呈現出各個t值的機率分布狀態之機率分配。
的所有可能樣本,計算出每一個樣本的t值與得到該t值的機率,最後呈現出各個t值的機率分布狀態之機率分配。
t分配會隨著樣本大小的不同而有不同的曲線,此點有別於不論樣本大小都只有一條曲線的常態分配。但當母群體本身為常態分配,或樣本數![]() 時,t分配會趨近於常態分配;當樣本數無限大的時候,t分配即變成常態分配的分配型態(參考下圖)。
時,t分配會趨近於常態分配;當樣本數無限大的時候,t分配即變成常態分配的分配型態(參考下圖)。
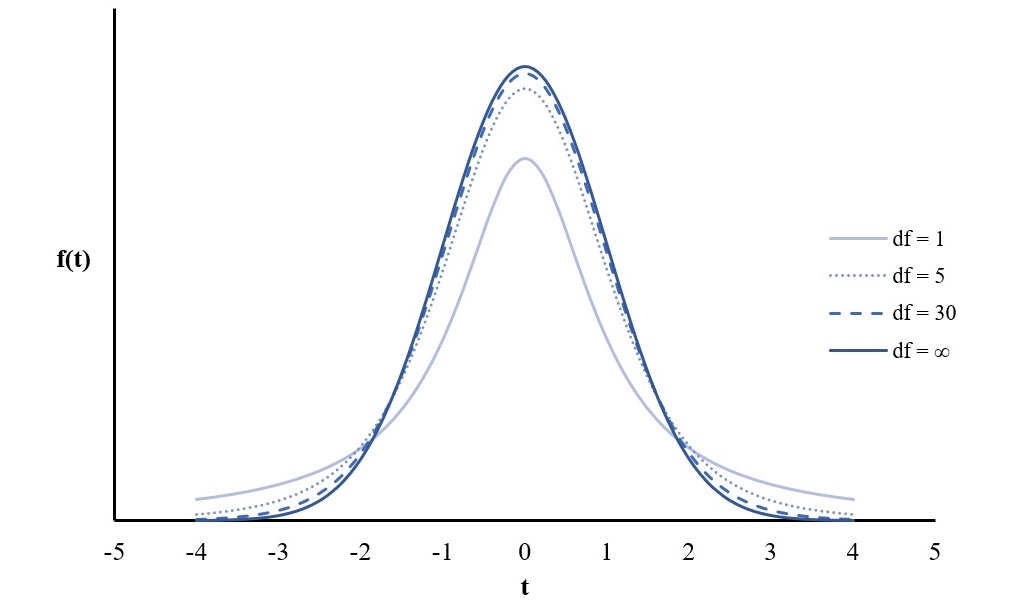
但t分配不是單純地因樣本數而有不同的曲線,它其實是隨著與樣本大小相關的自由度(degrees of freedom,簡稱df)而改變。自由度是指計算一個統計量時,可以自由變動的分數之數目。舉例來說,假設有5個分數且已知平均數為10,若隨意選擇了4個分數,分別為4、6、12、18,則第5個分數必定為10才能讓平均數為10;也就是說,能夠自由變動的分數個數為4,代表自由度為4。因此,若讓一個參數保持恆定,自由度必定為計算這個參數的分數之數目減去1。
小樣本或![]() 未知的信賴區間之計算須使用到t分配和單一樣本t值的計算方法,而單一樣本t值的計算公式如下:
未知的信賴區間之計算須使用到t分配和單一樣本t值的計算方法,而單一樣本t值的計算公式如下:
(1) 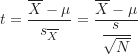
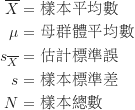
從上面的公式(1)可看出,因為計算t值時須先計算出樣本標準差![]() 而失去1個自由度,所以t的自由度為
而失去1個自由度,所以t的自由度為![]() 。這個自由度與t分配的曲線型態息息相關,也是下面提到的t分配表查詢時必須知道的訊息之一。
。這個自由度與t分配的曲線型態息息相關,也是下面提到的t分配表查詢時必須知道的訊息之一。
小樣本或σ未知的信賴區間
當母群體標準差![]() 未知或樣本數目很小時,並無法使用常態分配和標準分數來計算信賴區間,而須使用t分配和t值來計算。標準分數和t值最大的差別在於,標準分數使用母群體標準差
未知或樣本數目很小時,並無法使用常態分配和標準分數來計算信賴區間,而須使用t分配和t值來計算。標準分數和t值最大的差別在於,標準分數使用母群體標準差![]() 來計算,而t值使用樣本標準差
來計算,而t值使用樣本標準差![]() 來計算。也就是說,小樣本或
來計算。也就是說,小樣本或![]() 未知的信賴區間計算是利用樣本標準差
未知的信賴區間計算是利用樣本標準差![]() 作為母群體標準差
作為母群體標準差![]() 的估計值。
的估計值。

將原本計算![]() 已知的信賴區間的標準分數z換成t,母群體標準差
已知的信賴區間的標準分數z換成t,母群體標準差![]() 換成樣本標準差
換成樣本標準差![]() ,即為小樣本或
,即為小樣本或![]() 未知時信賴區間的計算方式,這時信賴區間的不等式如下:
未知時信賴區間的計算方式,這時信賴區間的不等式如下:
(2) ![]()
上面的不等式裡,![]() 為信賴區間的機率值,最常使用的機率值為0.95或0.99,也就是95%或99%信心程度。從上面的不等式可看出信賴界限分別為:
為信賴區間的機率值,最常使用的機率值為0.95或0.99,也就是95%或99%信心程度。從上面的不等式可看出信賴界限分別為:
- 下信賴限:
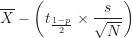
- 上信賴限:
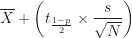
要找到t值,須使用t分配表,下表為部分的t分配表。實際上,t分配表包含「雙尾檢定的顯著水準」和「單尾檢定的顯著水準」兩部分,由於信賴區間的計算僅使用「雙尾檢定的顯著水準」,所以這裡沒有列出「單尾檢定的顯著水準」的表格內容。另外,表格最左邊的欄(df)為自由度,為樣本總數減去1(![]() )。
)。
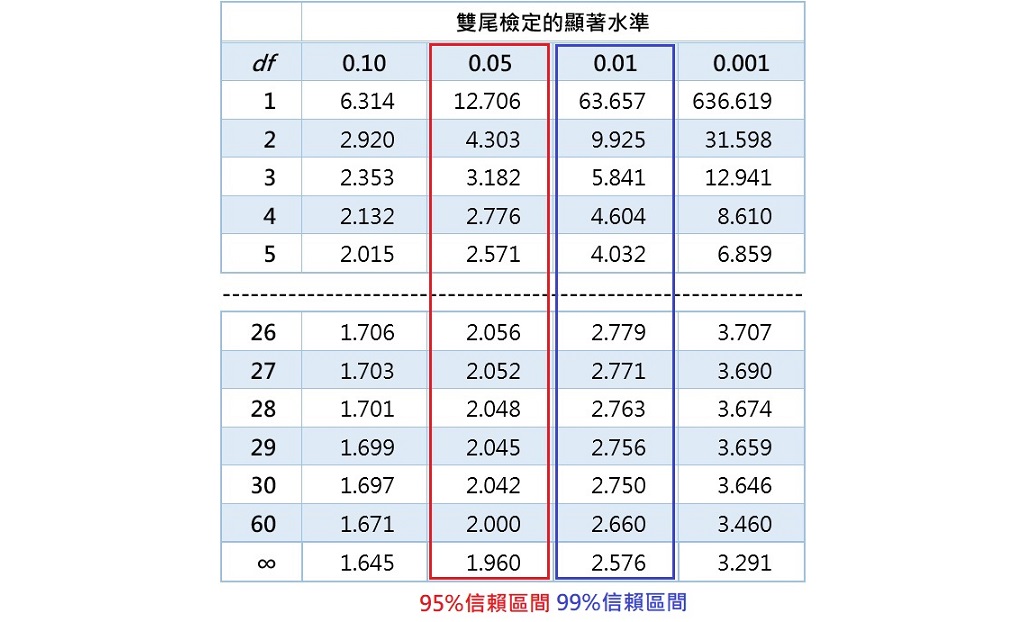
舉例來說,若樣本總數![]() 為27,想找95%的信賴區間,則顯著水準為
為27,想找95%的信賴區間,則顯著水準為![]() ,自由度為
,自由度為![]() ,查詢上表後得到的t值為2.056。
,查詢上表後得到的t值為2.056。
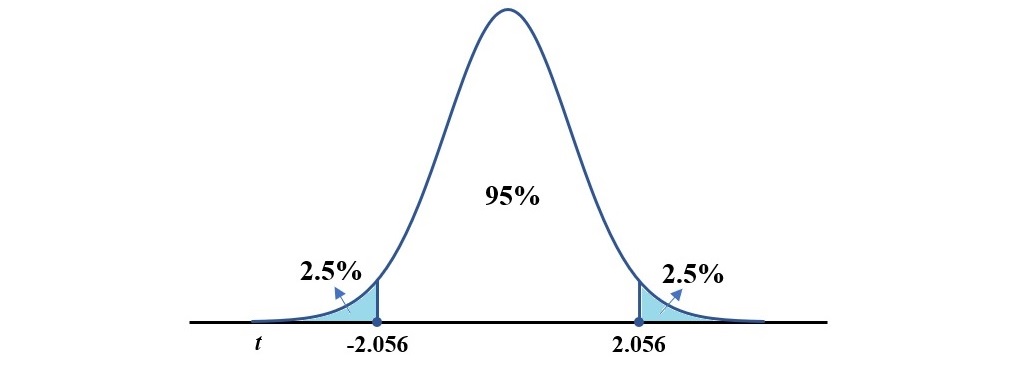
將t值2.056帶入上面的不等式(2),當樣本數目![]() 為27時,95%信賴區間的不等式如下:
為27時,95%信賴區間的不等式如下:
![]()
假設樣本數目![]() 同樣為27,但改成找99%的信賴區間,此時顯著水準為
同樣為27,但改成找99%的信賴區間,此時顯著水準為![]() ,自由度為
,自由度為![]() 。查詢上面的t分配表,得到的t值為2.779。
。查詢上面的t分配表,得到的t值為2.779。
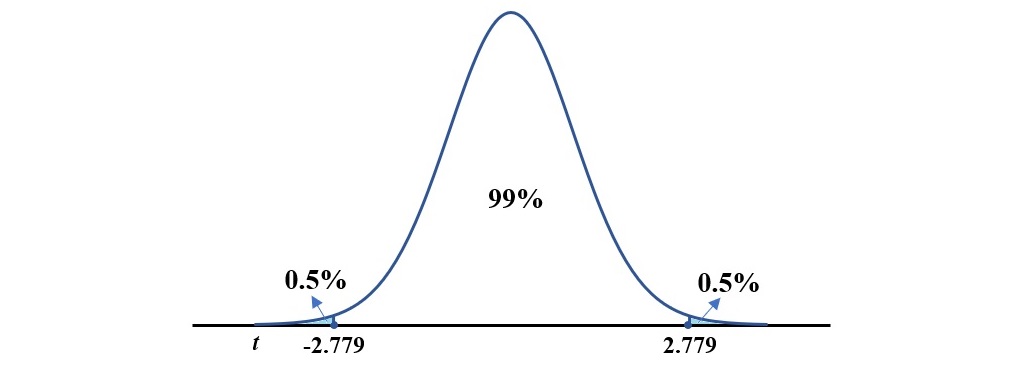
同樣地,將t值2.779帶入上面的不等式(2)。當樣本數目![]() 為27時,99%信賴區間的不等式為:
為27時,99%信賴區間的不等式為:
![]()
接著,只要再計算出樣本的平均數和標準差,並分別帶入上面95%和99%信賴區間的不等式中,就可得到樣本數目![]() 為27時的信賴區間。下面舉一個例子來示範
為27時的信賴區間。下面舉一個例子來示範![]() 未知時95%和99%信賴區間的計算過程。
未知時95%和99%信賴區間的計算過程。
σ未知時信賴區間的實例演算
假設一位英文老師想知道她所任職的學校裡高三生的平均英文能力,於是她隨機抽取出30位高三的學生,並給予他們英文能力測驗,成績如下表所示。試問該校高三生的平均英文能力測驗成績的95%和99%信賴區間各為何?

從題目可知母群體的標準差![]() 未知,須使用樣本標準差
未知,須使用樣本標準差![]() 作為
作為![]() 的估計值。因此,先計算出這30位學生成績的平均數
的估計值。因此,先計算出這30位學生成績的平均數![]() 和標準差
和標準差![]() ,計算方式請分別參考〈集中趨勢的測量〉裡平均數的計算和〈變異性的測量〉裡標準差的計算。
,計算方式請分別參考〈集中趨勢的測量〉裡平均數的計算和〈變異性的測量〉裡標準差的計算。
![]()
得到樣本的平均數和標準差後,就可利用上面的不等式(2),分別計算該校高三生平均英文能力測驗的95%和99%信賴區間,以下分別示範計算過程。
95%信賴區間
因為是95%信賴區間,所以「雙尾檢定的顯著水準」為![]() 。此外,樣本總數為30,所以自由度為
。此外,樣本總數為30,所以自由度為![]() 。查詢上面的t分配表,得到t的數值為2.045。
。查詢上面的t分配表,得到t的數值為2.045。
將![]() 、
、![]() 、
、![]() 、
、![]() 等數值帶入上面的不等式(2)裡:
等數值帶入上面的不等式(2)裡:
![Rendered by QuickLaTeX.com \begin{align*}\overline X - \left ( t_{\frac {1-p}{2}} \times \frac {s}{\sqrt N} \right ) \leq &\mu \leq \overline X + \left ( t_{\frac {1-p}{2}} \times \frac {s}{\sqrt N} \right ) \\[10pt]65.93 - \left ( 2.045 \times \frac {13.48}{\sqrt {30}} \right ) \leq &\mu \leq 65.93 + \left ( 2.045 \times \frac {13.48}{\sqrt {30}} \right ) \\[10pt]60.90 \leq &\mu \leq 70.97\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-0bf0aa63248945b7076cd1f400535a1b_l3.png)
從計算結果得知,信賴下限為60.90分,信賴上限為70.97分。換句話說,有0.95的機率或95%的信心程度,該校高三生的平均英文能力測驗成績落在60.90分和70.97分之間。
99%信賴區間
因為是99%信賴區間,所以「雙尾檢定的顯著水準」為![]() 。此外,樣本總數為30,所以自由度為
。此外,樣本總數為30,所以自由度為![]() 。查詢上面的t分配表,找到t值為2.756。
。查詢上面的t分配表,找到t值為2.756。
將![]() 、
、![]() 、
、![]() 、
、![]() 等數值帶入上面的不等式(2)裡:
等數值帶入上面的不等式(2)裡:
![Rendered by QuickLaTeX.com \begin{align*}\overline X - \left ( t_{\frac {1-p}{2}} \times \frac {s}{\sqrt N} \right ) \leq &\mu \leq \overline X + \left ( t_{\frac {1-p}{2}} \times \frac {s}{\sqrt N} \right ) \\[10pt]65.93 - \left ( 2.756 \times \frac {13.48}{\sqrt {30}} \right ) \leq &\mu \leq 65.93 + \left ( 2.756 \times \frac {13.48}{\sqrt {30}} \right ) \\[10pt]59.15 \leq &\mu \leq 72.71\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-15555e5197fece7e7fe819adc88ead18_l3.png)
計算結果顯示,信賴下限為59.15分,而信賴上限為72.71分。這個結果指出,有0.99的機率或99%的信心程度,該校高三生的平均英文能力測驗成績落在59.15分和72.71分之間。
雖然使用紙筆運算並不困難,但每次計算都須先求得資料的平均數、標準差,再查詢t分配表去找到t值,整個過程有些麻煩,此時若使用統計分析軟體來進行運算將會節省許多時間,下面示範利用 SPSS 求得![]() 未知的信賴區間之操作方法。
未知的信賴區間之操作方法。
運用 SPSS 求得σ未知的信賴區間
將上面實例的30個分數(變項名稱為 SCORE)輸入至 SPSS 的資料編輯器中,輸入完成後,點選功能表的分析 » 比較平均數 » 單一樣本T檢定,帶出「單樣本T檢定」視窗。關於 SPSS 的資料輸入方法,請參考 SPSS操作環境和資料輸入。
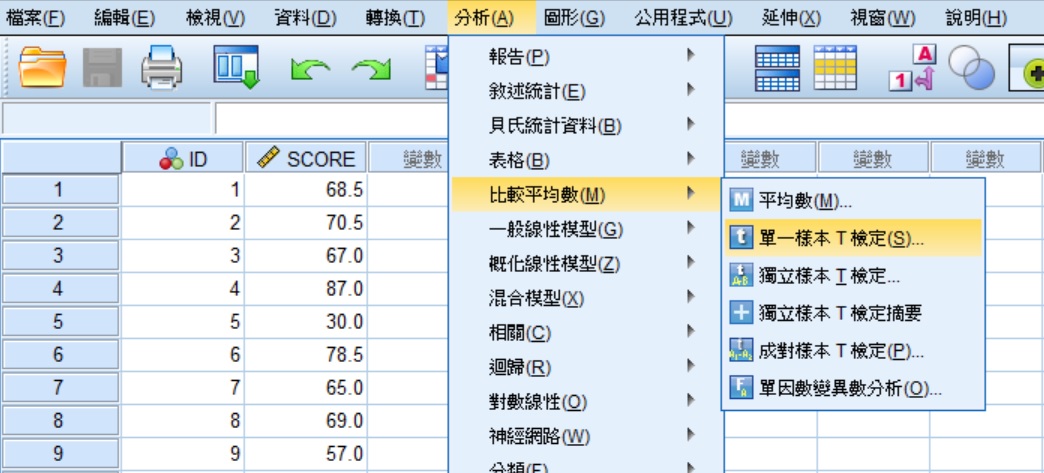
不同信心程度的信賴區間僅在於不同信賴區間百分比數值的輸入,其餘的操作過程都相同,以下分別示範95%和99%信賴區間的操作過程。
95%信賴區間
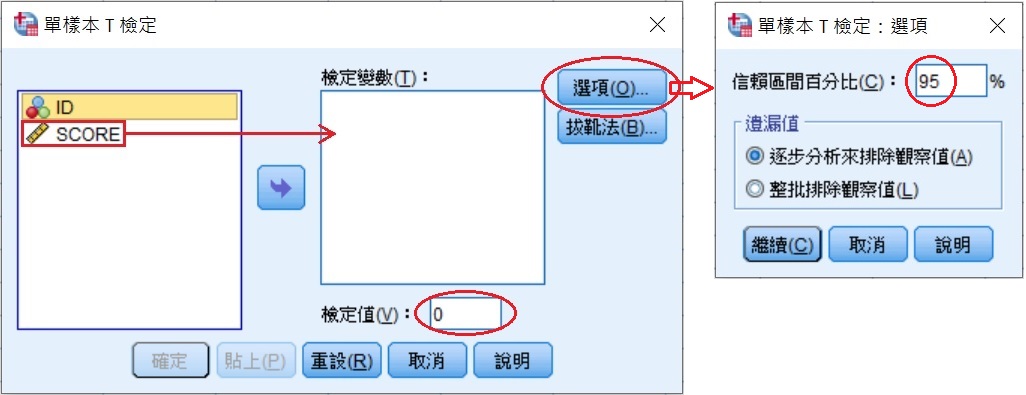
在「單樣本T檢定」視窗中,將 SCORE 移至檢定變數(T)方框中,下方的檢定值(V)設為0。接著,點選視窗右側的選項(O),在隨即出現的「單樣本T檢定:選項」小視窗中,信賴區間百分比(C)填入95,完成後按下方的繼續(C),回到上一個視窗後再按下確定。
經過上面的步驟,SPSS 會輸出2個表格,第1個表格為變項 SCORE 的描述統計量,包括樣本總數、樣本平均數、樣本標準差和估計標準誤。從下表可看出,這30位學生的平均成績為65.93分,標準差為13.48,估計標準誤為2.46。

第2個表格為單一樣本t檢定的結果,可略過t值和顯著性的結果,直接看95%信賴區間的資訊。下表的95%信賴區間顯示,下信賴限為60.90分,上信賴限為70.97分,也可看到自由度為29,這些結果全都和上面紙筆計算的結果相同。

分析結果告訴我們有0.95的機率或95%的信心程度,這個學校高三生的平均英文能力測驗成績會落在60.90分和70.97分之間。若要使用美國心理學會論文格式(簡稱為 APA 格式)來撰寫95%信賴區間的結果,可用 95% CI [60.90, 70.97] 來表示,中括弧裡先寫下信賴限再寫上信賴限。
99%信賴區間
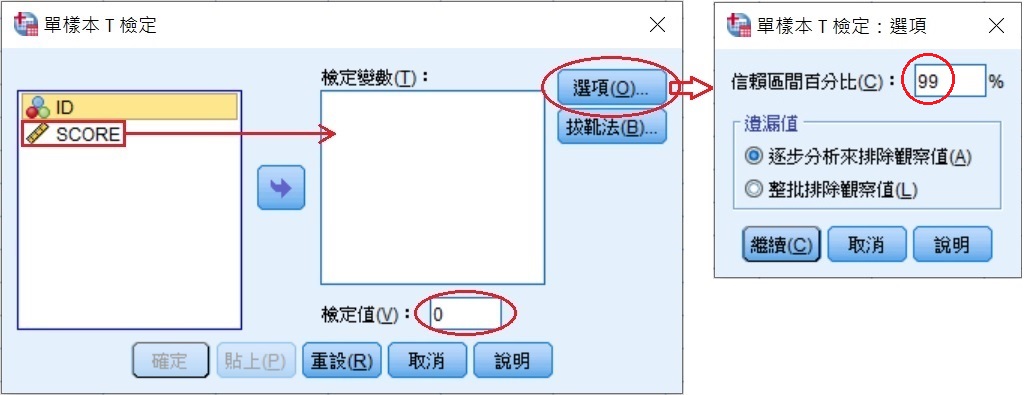
若要求得99%信賴區間,在「單樣本T檢定:選項」小視窗中,信賴區間百分比(C)填入99,按下繼續(C),回到「單樣本T檢定」視窗後,再按下最下方的確定。
同樣地,SPSS 會輸出2個表格,這裡略過第1個描述統計量的表格,直接看第2個「單一樣本檢定」表格。從下表可看到99%信賴區間的下信賴限為59.15分,而上信賴限為72.72分。雖然上信賴限的值較紙筆計算的值多0.01,但這是進位誤差所導致,並不影響整體的分析結果。

上表的結果顯示,有0.99的機率或99%的信心程度,這個學校高三生的平均英文能力測驗成績會落在59.15分和72.72分之間。若要使用 APA 格式來撰寫99%信賴區間的分析結果,寫法為 99% CI [59.15, 72.72],中括弧裡先寫下信賴限再寫上信賴限。
若您沒有 SPSS 或其他的統計分析軟體,也可利用微軟的 Excel 來計算信賴區間。Excel 內建2個信賴區間函數,分別為 CONFIDENCE.NORM 函數和 CONFIDENCE.T 函數,前者適用在樣本數較大且母群體標準差已知時,而後者適用在樣本數較小或母群體標準差未知的時候,詳細的操作方法可以參考如何使用Excel計算信賴區間。
以上為本篇文章對於小樣本或![]() 未知時信賴區間計算的介紹,希望透過本篇文章,您瞭解了t分配的意義、利用t分配和t值計算信賴區間的方法,也學會了如何運用 SPSS 求得小樣本或
未知時信賴區間計算的介紹,希望透過本篇文章,您瞭解了t分配的意義、利用t分配和t值計算信賴區間的方法,也學會了如何運用 SPSS 求得小樣本或![]() 未知時的信賴區間。若您喜歡本篇文章,請將本網站加入書籤,並持續回訪本網站喔!另外,也歡迎您追蹤本網站的 Facebook 和 X(Twitter)專頁喲!
未知時的信賴區間。若您喜歡本篇文章,請將本網站加入書籤,並持續回訪本網站喔!另外,也歡迎您追蹤本網站的 Facebook 和 X(Twitter)專頁喲!
如果您覺得本篇文章對您有幫助,歡迎買杯珍奶給 Dr. Fish!小小珍奶,大大鼓勵,您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔!