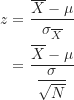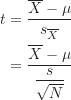🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
單一樣本t檢定的假設檢定
單一樣本t檢定(one-sample t-test)的假設檢定和單一樣本z檢定的假設檢定相當類似,都是用來檢驗一個樣本平均數是否來自於特定母群體的虛無假設,兩者最主要的差別在於母群體標準差是否為已知的狀態。
t檢定是由William S. Gosset以Student的筆名所提出,所以也稱為Student´s t檢定。在行為或社會科學的研究領域裡,t檢定是一個很強大且常被使用的統計檢定方法,包含單一樣本t檢定、獨立樣本t檢定和關聯樣本t檢定,本篇文章將針對單一樣本t檢定做詳細的介紹。
由於下面的內容牽涉到假設檢定,若您不清楚或不熟悉假設檢定的過程,建議您先閱讀假設檢定的步驟和範例,將有助於文章內容的理解。以下將先說明單一樣本t檢定和單一樣本z檢定的差異,再介紹t抽樣分配和單一樣本t檢定的假設檢定,並舉例說明,最後示範利用SPSS執行單一樣本t檢定的操作方法。
單一樣本t檢定和單一樣本z檢定的比較
單一樣本t檢定和單一樣本z檢定同樣用來比較一個樣本平均數和一個已知的母群體平均數,但不同於單一樣本z檢定是在母群體標準差已知的情況下使用,單一樣本t檢定是在母群體標準差未知的情況下使用。因為母群體標準差未知,所以單一樣本t檢定用樣本標準差估計母群體標準差。下表為兩者公式的比較:
| 單一樣本z檢定 | 單一樣本t檢定 |
|---|---|
|
|
|
|
|
|
從上表可看出,兩個公式的分子並無不同,差別在於分母的計算。單一樣本z檢定公式的分母為母群體標準差![]() 除以
除以![]() ,而單一樣本t檢定公式的分母為樣本標準差
,而單一樣本t檢定公式的分母為樣本標準差![]() 除以
除以![]() 。也就是說,單一樣本t檢定用估計平均數標準誤
。也就是說,單一樣本t檢定用估計平均數標準誤![]() 取代平均數標準誤
取代平均數標準誤![]() 。
。
另外一個差別在於樣本的大小。使用單一樣本z檢定時,樣本數須等於或大於30,然而單一樣本t檢定則可使用在樣本數小於30的情況。
簡單來說,當![]() 且母群體標準差
且母群體標準差![]() 已知時,使用單一樣本z檢定;但當
已知時,使用單一樣本z檢定;但當![]() 或母群體標準差
或母群體標準差![]() 未知時,則須使用單一樣本t檢定。
未知時,則須使用單一樣本t檢定。
由於單一樣本t檢定適用在小樣本上,所以假設檢定不適用單一樣本z檢定的常態分配,而須使用t抽樣分配。雖然t抽樣分配和常態分配一樣,都是對稱的分配型態,但具有獨特的特性,下面來看看t抽樣分配的特性。
t抽樣分配
t抽樣分配(sampling distribution of ![]() )是指從母群體中隨機抽取出樣本大小為
)是指從母群體中隨機抽取出樣本大小為![]() 的所有可能樣本,計算出每一個樣本的t值和獲得該t值的機率,最後呈現出各個t值的機率分布狀態之機率分配。關於抽樣分配的概念,請參考平均數抽樣分配的定義和特性。
的所有可能樣本,計算出每一個樣本的t值和獲得該t值的機率,最後呈現出各個t值的機率分布狀態之機率分配。關於抽樣分配的概念,請參考平均數抽樣分配的定義和特性。
不像z分配僅有一條曲線(常態曲線),t分配會隨著樣本大小而有不同的曲線。當樣本數等於或大於30時,t分配就會趨近於常態分配。但更正確地說,t分配是隨著自由度(degrees of freedom,簡寫為df)的改變而有不同的曲線,而非單純地因為樣本大小而改變。
自由度是指計算一個統計量時,可以自由變動的分數個數。舉例來說,若隨機從一母群體裡抽取出5個分數,這5個分數都可自由地變動。但若已知平均數為15,則不可能5個分數皆可自由地變動,假設前4個分數為5、10、15、20,最後一個分數必定為25,才能使平均數為15,因此自由度為4(![]() )。
)。
因為曲線會隨著自由度而改變,所以t分配有很多條曲線,如下圖。t分配為對稱的鐘形曲線,且平均數為0,可用來決定得到一個特定數值的機率值。自由度愈高時,曲線會愈接近常態分配的曲線型態。當自由度等於30時,t分配已趨近於常態分配;當自由度無限大時,t分配和常態分配已全然相同。
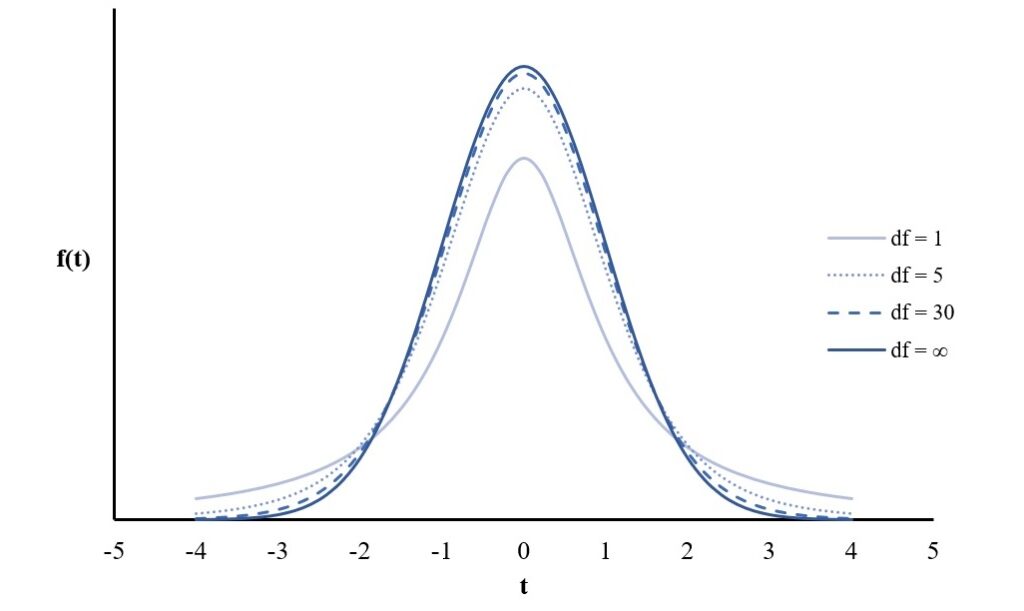
單一樣本t檢定的假設檢定和單一樣本z檢定的假設檢定沒有太大的不同,最主要的差別在於不同抽樣分配和檢定統計量的使用。前者使用t抽樣分配和t檢定統計量,而後者使用常態分配和z檢定統計量,下面就來說明單一樣本t檢定的假設檢定過程。
單一樣本t檢定的假設檢定
單一樣本t檢定用來比較一個樣本平均數![]() 是否顯著地不同於一個已知的母群體平均數
是否顯著地不同於一個已知的母群體平均數![]() ,且母群體標準差
,且母群體標準差![]() 是未知的情況。對立假設(
是未知的情況。對立假設(![]() )可為無方向性或有方向性,端視研究目的而定。有關研究假設的詳細介紹,請參考研究假設的種類和寫法。
)可為無方向性或有方向性,端視研究目的而定。有關研究假設的詳細介紹,請參考研究假設的種類和寫法。
根據研究的性質、目的,選擇適當的顯著水準(α水準),通常為0.05、0.01或更嚴苛的0.001。再依據已擬定好的研究假設,決定假設檢定為單尾檢定或雙尾檢定。關於顯著水準、單尾和雙尾檢定的詳細說明,請參考顯著水準和決策規則。
單一樣本t檢定的檢定統計量為t檢定統計量,分子為樣本平均數和母群體平均數的差值,分母為樣本標準差除以![]() 。公式如下:
。公式如下:
(1) 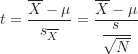
藉由事先選擇好的α水準,查詢t分配表,自由度為![]() ,找出相對應的臨界值,並比較t檢定統計量和臨界值。若研究假設不具方向性(雙尾檢定),當t檢定統計量的絕對值等於或大於臨界值的絕對值時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
,找出相對應的臨界值,並比較t檢定統計量和臨界值。若研究假設不具方向性(雙尾檢定),當t檢定統計量的絕對值等於或大於臨界值的絕對值時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
若使用統計分析軟體來執行單一樣本t檢定,通常會輸出獲得該特定t檢定統計量的機率值(![]() 值),反而省卻了查詢表格的麻煩。機率比較的決策規則為,當
值),反而省卻了查詢表格的麻煩。機率比較的決策規則為,當![]() 值小於或等於α水準(
值小於或等於α水準(![]() )時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
)時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
若使用有方向性的研究假設(單尾檢定),須注意t檢定統計量和對立假設的方向要一致,否則就應保留虛無假設。例如對立假設為樣本平均數小於母群體平均數,計算出來的t檢定統計量須為負數,才能進一步比較t檢定統計量和臨界值。反之,若t檢定統計量為正數,因為和對立假設的方向相反,所以須保留虛無假設。
單一樣本t檢定用來比較一個樣本平均數和一個已知的母群體平均數,操作上並不困難,但在使用前資料須滿足下述的兩個條件:
- 統計量為平均數:基本統計量為一個樣本平均數
 ,且母群體平均數
,且母群體平均數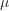 已知,但母群體標準差
已知,但母群體標準差 未知。
未知。 - 抽樣分配為常態分配:平均數抽樣分配須呈現常態分配,也就是樣本數等於或大於30,或樣本來自的母群體呈現常態分配。
瞭解了單一樣本t檢定的假設檢定步驟後,接著舉一個例子來實際操作單一樣本t檢定的假設檢定過程。
單一樣本t檢定的範例
有一位大學心理學教師向學生介紹一種有效率的學習方法,並要求學生付諸實行。兩個星期後,她向班上的9位學生發放問卷,調查學生的學習行為,分數愈高代表學生的讀書時間較長且運用了她介紹的學習方法,9位學生的分數如下表。該位教師在過往的教學紀錄顯示問卷的平均分數為68分,她想探討今年學生的學習行為是否不同於過往的學生。

因為該位教師想瞭解今年學生的學習行為「是否不同於」過往的學生,所以研究假設為無方向性的假設,對立假設和虛無假設的寫法如下:
- 對立假設(
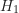 ):今年學生的學習行為不同於過往的學生。也就是說,今年的學生來自於
):今年學生的學習行為不同於過往的學生。也就是說,今年的學生來自於 的母群體。
的母群體。 - 虛無假設(
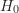 ):今年學生的學習行為相同於過往的學生。也就是說,今年的學生來自於
):今年學生的學習行為相同於過往的學生。也就是說,今年的學生來自於 的母群體。
的母群體。
由於這位老師只是想瞭解今年學生的學習行為,所以選擇了0.05的α水準。另外,因為研究假設沒有方向性,所以使用雙尾檢定,若用符號來表示,可以寫成![]() 。
。
因為研究問題為一個樣本平均數(今年學生的問卷平均分數)是否顯著地異於一個已知的母群體平均數(過往學生的問卷平均分數),再加上母群體標準差未知,且樣本數小於30,所以選擇單一樣本t檢定和t抽樣分配,其檢定統計量為t檢定統計量。
由於計算t檢定統計量時,需要樣本平均數和標準差,所以這裡先計算出9位學生的問卷平均數和標準差。這9位學生的問卷平均數為:
![]()
標準差的計算需要每個分數和平均數間的離差![]() ,以及每一個分數的離差平方
,以及每一個分數的離差平方![]() ,可先在如下的表格裡計算出來。
,可先在如下的表格裡計算出來。
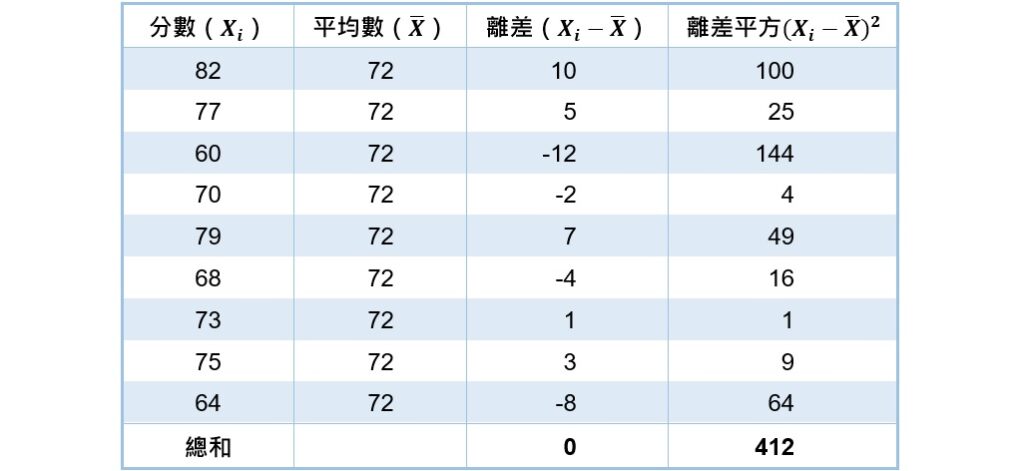
接著,將上表中每一個分數的離差平方加起來,再把總和帶入樣本標準差的公式裡:
![Rendered by QuickLaTeX.com \[ s=\sqrt {\frac {\sum \limits_{i=1}^n (X_i-\overline X)^2}{N-1}}=\sqrt {\frac {412}{9-1}} \approx 7.17635 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-e50fbd62d8f2fb6af118e1ca3456cb39_l3.png)
最後,將已經計算出來的樣本平均數和標準差帶入上面t檢定統計量的公式(1)裡:
![Rendered by QuickLaTeX.com \[ t=\frac {\overline X-\mu}{\displaystyle \frac {s}{\sqrt N}}=\frac {72-68}{\displaystyle \frac {7.17635}{\sqrt 9}}=\frac {4}{2.39212} \approx 1.672 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-eea2f37fd6b2bf4df1a7b2a17fd1f19b_l3.png)
計算結果顯示t檢定統計量為1.672。然後,查詢t分配表,當α水準為0.05、雙尾檢定、自由度為8(![]() )時,t臨界值為
)時,t臨界值為![]() 。
。
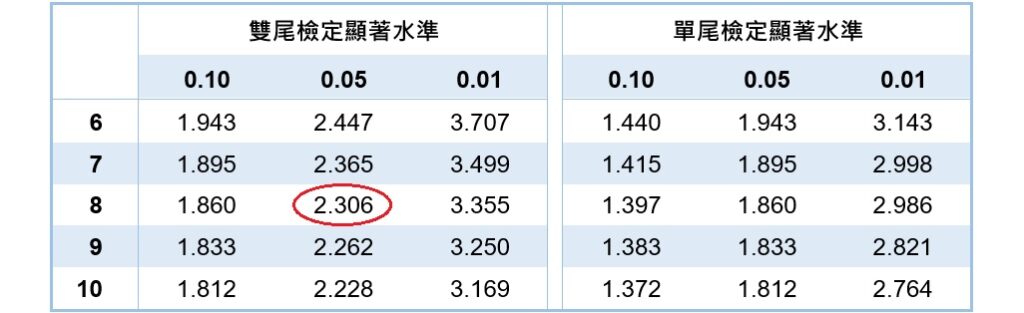
比較t檢定統計量的絕對值和t臨界值的絕對值,依據決策規則,因為![]() ,所以保留虛無假設。分析結果顯示,今年學生的學習行為和過往學生的學習行為並無不同。
,所以保留虛無假設。分析結果顯示,今年學生的學習行為和過往學生的學習行為並無不同。
若使用統計分析軟體執行單一樣本t檢定,軟體會輸出獲得t檢定統計量的機率值,決策規則可改成![]() 值和α水準的比較。以下示範利用SPSS執行單一樣本t檢定的過程,以及如何解釋輸出表格裡的數據。
值和α水準的比較。以下示範利用SPSS執行單一樣本t檢定的過程,以及如何解釋輸出表格裡的數據。
運用SPSS執行單一樣本t檢定
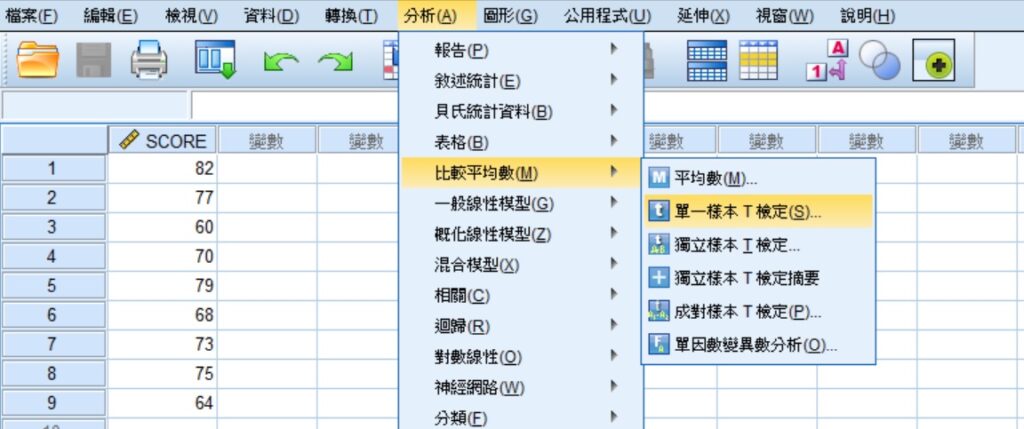
將上面範例中的9個分數輸入至SPSS資料編輯器裡,變項名稱為SCORE。輸入完成後,點選功能表的分析 » 比較平均數 » 單一樣本T檢定,帶出「單樣本T檢定」視窗。關於SPSS的資料輸入方法,請參考SPSS操作環境和資料輸入。
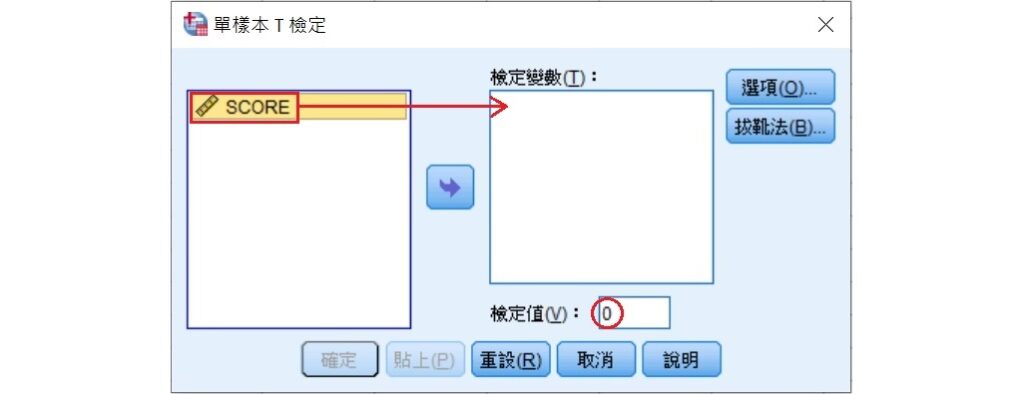
在「單樣本T檢定」視窗中,將左邊方框中的變項SCORE移至右邊檢定變數(T)的方框裡。該方框正下方的檢定值(V)是指母群體平均數的數值,此處為68,所以在該欄位輸入68。
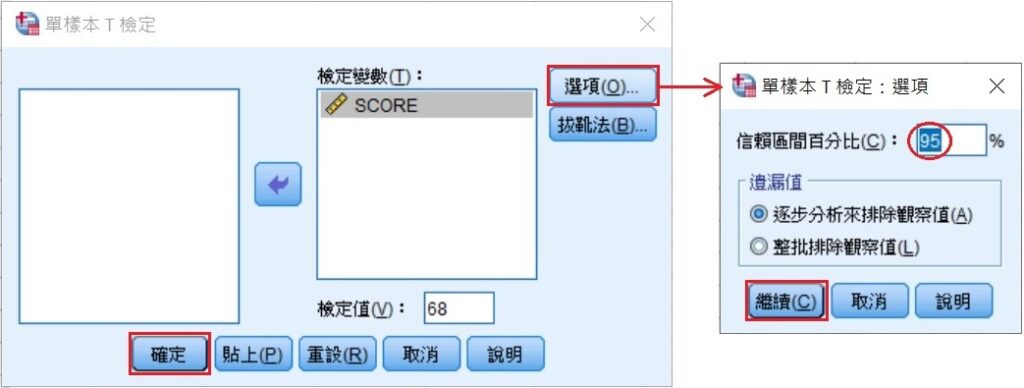
在「單樣本T檢定」視窗的最右邊有個選項(O),點選後會出現「單樣本T檢定:選項」小視窗,該視窗裡的信賴區間百分比(C)指α水準的設定。若α水準為0.05,在該欄位輸入95;若α水準為0.01,則輸入99。輸入完成後,點選繼續(C),回到上一個視窗後再點選確定。
經過上面的步驟,SPSS會輸出兩個表格,第1個為「單一樣本統計量」表,第2個為「單一樣本檢定」表。第1個「單一樣本統計量」表格為樣本的描述統計量,從下表可看出,樣本總個數為9、樣本平均數為72、樣本標準差為7.176,標準誤平均值(SPSS的翻譯有點奇怪,應是「平均數標準誤」)即是標準差除以![]() (
(![]() ),也是t檢定統計量公式的分母。
),也是t檢定統計量公式的分母。

第2個「單一樣本檢定」表格為單一樣本t檢定的分析結果,該表格顯示樣本平均數和母群體平均數的差值為4、自由度為8、t檢定統計量為1.672,而獲得該統計量的機率為0.133。

依據決策規則,若![]() ,即可拒絕虛無假設,接受對立假設。獲得t檢定統計量的
,即可拒絕虛無假設,接受對立假設。獲得t檢定統計量的![]() 值為0.133,α水準為0.05,因為
值為0.133,α水準為0.05,因為![]() ,所以保留虛無假設。分析結果顯示,今年學生的學習行為並沒有不同於過往學生的學習行為。
,所以保留虛無假設。分析結果顯示,今年學生的學習行為並沒有不同於過往學生的學習行為。
因此,不論是透過紙筆計算的檢定統計量和臨界值的比較,或藉由統計分析軟體的![]() 值和α水準的比較,都可得到相同的分析結果。另外,有一點須注意的是,SPSS輸出的機率值為雙尾檢定的機率值,若要使用單尾檢定,必須將機率值除以2後,再與α水準做比較。
值和α水準的比較,都可得到相同的分析結果。另外,有一點須注意的是,SPSS輸出的機率值為雙尾檢定的機率值,若要使用單尾檢定,必須將機率值除以2後,再與α水準做比較。
以上為本篇文章對單一樣本t檢定的介紹,希望透過本篇文章,您瞭解了單一樣本t檢定的使用時機、t抽樣分配的特性和單一樣本t檢定的假設檢定過程,也學會了利用SPSS執行單一樣本t檢定的操作方法。
若您喜歡本篇文章,請將本網站加入書籤,作為您的學習資源,並持續回訪本網站喔!另外,您也可以在Facebook和Twitter上找到我們喲!