測量尺度的意義和分類

統計資料（或稱統計數據）是透過測量或蒐集所得到的結果，可能具有多種不同的類型和複雜的層次，而測量尺度（scales/levels of measurement）就是用來指出被測量的內容和代表被測量內容的數值之間的關係，是社會統計裡一個很重要的基礎概念。

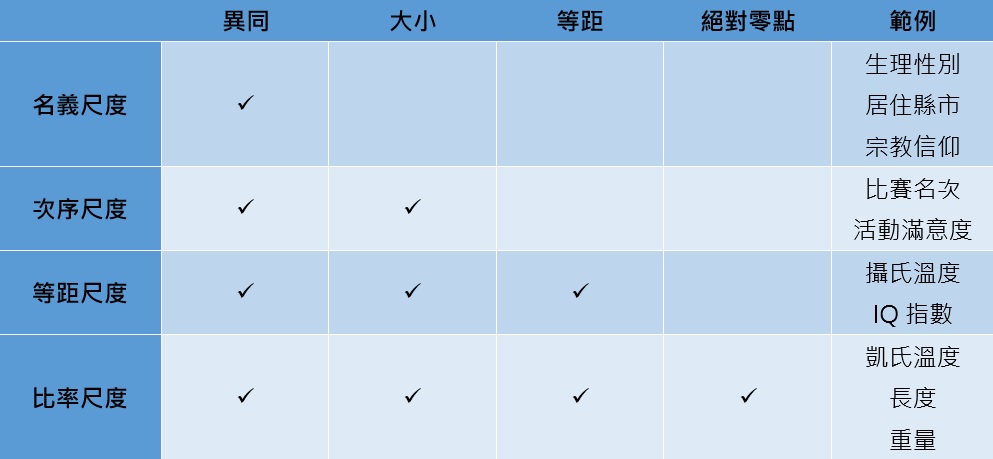
每一種測量尺度都有其數學屬性，而且決定之後可使用的統計檢定方式。理論上，測量尺度的數學屬性包括大小、等距和絕對零點（absolute zero point），而一種測量尺度可能具備一個或多個數學屬性。依據數學屬性的多寡，測量尺度從最低到最高層次依序為名義尺度、次序尺度、等距尺度與比率尺度，以下將分別說明這4種測量尺度，並介紹在SPSS裡調整測量尺度的方法。

測量尺度的分類
SPSS測量尺度的調整欄位

測量尺度的分類

1. 名義尺度（nominal scale）

名義尺度為最低層次的測量尺度，通常為質性的變項（variable）。名義尺度的變項被劃分為數個互斥的類別，受測對象在接受測量後被歸入其所屬的類別，這些類別即構成該名義尺度變項的組成單元。最基本的類型為僅有兩個類別的變項，通常稱為二元變項（binary variable）或二分變項（dichotomous variable），例如生理女性和男性、活著和死亡、有工作和沒有工作。

名義尺度變項的各個互斥類別間只有異同，並沒有大小之分，也沒有等距和絕對零點等數學屬性，但在分析上可計算出各個類別的數量，也就是次數分配。例如可分為生理女性和男性的生理性別，並無法區分大小，但為了統計分析的方便，可將生理男性編碼為1、生理女性編碼為2，藉此來計算兩者個別的人數。

2. 次序尺度（ordinal scale）

次序尺度為高於名義尺度一個層次的測量尺度。次序尺度變項的各個類別間不僅有異同，還有大小之分，所以可進行排序，用來決定 $A>B$ 、 $A=B$ 或 $A<B$ 。

不過，次序尺度變項雖然可以進行大小、高低、優劣或多寡等比較，卻無法說明差異的確切大小，也就是不具備等距的數學屬性。例如馬拉松比賽的名次，第1名的完賽時間少於第2名，第2名的完賽時間少於第3名，但第1名與第2名的時間差距不一定相同於第2名與第3名的時間差距。

3. 等距尺度（interval scale）

等距尺度為高於次序尺度一層次的測量尺度。除了具備次序尺度的大小（能夠排序）特質外，等距尺度變項同時具有等距的數學屬性，也就是相鄰單位之間具有相等的變化量，但沒有絕對零點的特性。

絕對零點為熱力學理論裡的最低溫度，為攝氏溫度（Celsius）零下273.15度，凱氏溫度（Kelvin）的0度，是指沒有溫度的狀態，此處意味著欲測量的現象不存在。

攝氏溫度即為等距尺度的例子，攝氏20度低於攝氏23度，攝氏23度低於攝氏26度，攝氏20度與23度之間的差異等於攝氏23度與26度之間的差異，但攝氏0度並不代表沒有溫度。因此，等距尺度不但可決定大小， $A<B$ 、 $A=B$ 或 $A>B$ ，也可決定相鄰單位之間是否具有相等的變化量， $A-B<C-D$ 、 $A-B=C-D$ 或 $A-B>C-D$ 。

4. 比率尺度（ratio scale）

比率尺度為最高層次的測量尺度，除了具有等距尺度的大小、等距之數學屬性外，還帶有絕對零點。因為有絕對零點的特質，所以能夠計算比率。

比率尺度的一個例子為凱氏溫度。不同於不具有絕對零點的攝氏溫度，凱氏溫度具有絕對零點，也就是完全沒有溫度的狀態，因此可用比率概念說明溫差，例如凱氏30度是凱氏15度的2倍熱。此外，長度、重量、年齡等也屬於比率尺度，皆可進行加、減、乘、除的數學運算。

因此，整體來說，名義尺度具有的特性最少，只能夠比較異同；而比率尺度具備的特性最多，不但可比較異同，還能夠進行加減乘除的數學運算。四種測量尺度的差異可用下表來呈現：

由於變項的測量尺度會影響統計檢定方法的選擇，所以使用統計分析軟體時，最好明確地指出每一個變項的測量尺度，以下簡單地介紹SPSS測量尺度的調整欄位。

SPSS測量尺度的調整欄位

SPSS資料編輯器的變數視圖頁面的測量欄位，可進行變項測量尺度的修改。在測量欄位，按一下儲存格右側的按鈕，下拉選單包含三種尺度：名義、序數和尺度（見下圖紅色框處）。名義即為名義尺度，序數為次序尺度，尺度則包括等距尺度和比率尺度。

雖然只要變項的數值具有順序且為有意義的計量（也就是可進行數值之間距離的比較），SPSS皆將他們歸類為尺度，但資料分析人員最好還是辨明變項為等距或比率尺度，才能夠選擇合適的統計檢定方式。關於SPSS的操作介面，可參考SPSS操作環境和資料輸入或直接點選本網頁右側邊列的圖示。

以上為本篇文章對測量尺度的意義和分類的說明，至於各種測量尺度的變項在社會統計分析裡的實際應用，將會在本網站的其他文章裡進行介紹喔！

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站喔。另外，也歡迎您追蹤我們的Facebook和Twitter專頁，將可獲得最新文章的資訊喲！