變異性的測量

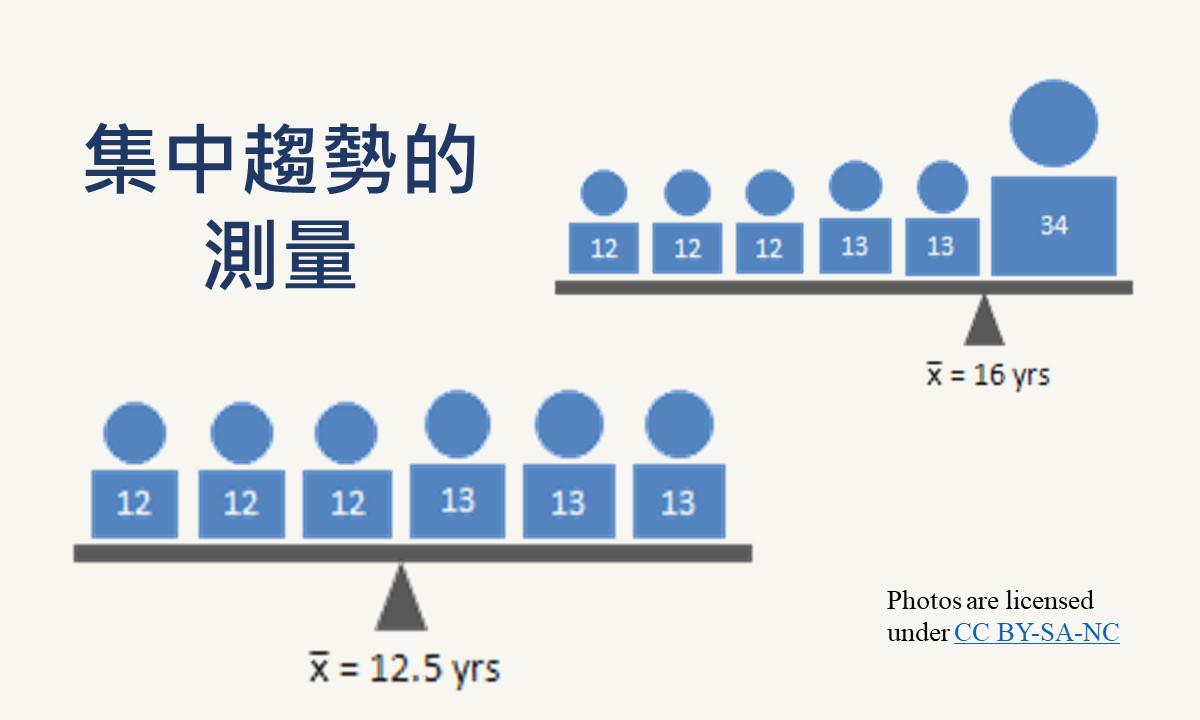
研究資料整理完成後的初步分析階段，通常會先瞭解數據資料的全貌，此時除了集中趨勢的測量外，還會進行變異性（variability）的測量。集中趨勢的測量是使用量化的數值來顯示資料的集中情況，而變異性的測量則是使用量化的數值來呈現資料的分散程度。

最常被使用的變異性測量方法有3種，分別為全距（range）、標準差（standard deviation）和變異數（variance），本篇文章將逐一介紹各個測量方法的意義和計算方式，以及如何使用SPSS或Excel來取得變異性測量的統計量。若您只對某部分的內容感興趣，可以點選下方的連結，即可直接跳至您想瞭解的內容喔。

變異性的測量方法
運用SPSS取得變異性測量的統計量
運用Excel取得變異性測量的統計量

變異性的測量方法

行為或社會科學研究最常使用的變異性測量方法有3種，分別為全距、標準差和變異數，以下將詳細介紹每一種測量方法。

全距

在分組分數次數分配文章中提到，若要進行數據資料的分組時，須先計算全距，即是將資料中的最大數值減去最小數值，而「全距」就是這裡所提到的第1種變異性測量方式。舉例來說，假設資料裡有11個數值，12、15、22、29、32、40、53、58、67、74、82，全距為 $82-12=70$ 。

由於全距的計算只使用到資料裡的最大值與最小值，所以很容易受到離群值或極端數值的影響。為了彌補此一缺點，有一個慣用的方法是去除頭尾各25%的數值，只使用中間50%的數值來計算四分位距（interquartile range）。

計算四分位距時，要先找到四分位數（quartiles），也就是能將排序好的數據資料平均劃分成四等分的三個數值。第一個數值是將所有資料平均劃分為兩等分的中位數（median），也稱為第二四分位數（second quartile）。第二個數值為前50%資料的中位數，稱為第一四分位數（lower quartile）；第三個數值為後面50%資料的中位數，稱為第三四分位數（upper quartile）。

習慣上，若數據資料的總個數為奇數，中位數不會被包含在前50%或後50%的資料中。參考下圖，以上述的11個數值為例，中位數（第二四分位數）為40，第一四分位數為22，第三四分位數為67。四分位距的計算方式為第三四分位數減去第一四分位數，也就是 $67-22=45$ 。

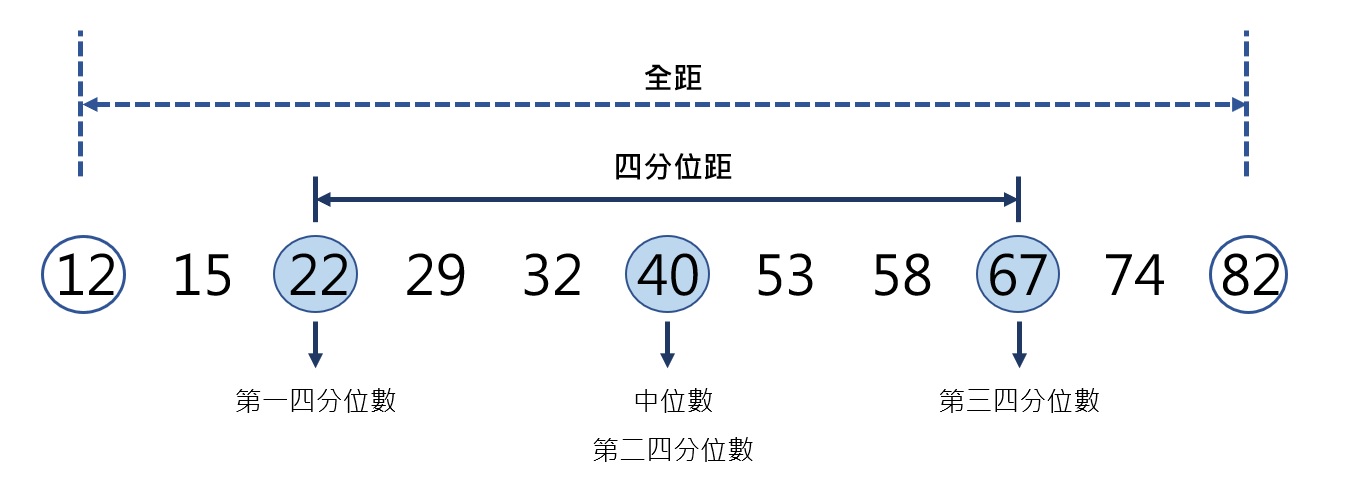
和全距相比較，雖然四分位距較不容易受到位於資料分配前端或後端的離群值之影響，但和全距的計算方式一樣，僅使用到數據資料裡的兩個數值來進行運算，而沒有考量到其他的數值，此為最大的缺點。

標準差

若要運用數據資料裡的每一個數值來找出分散程度，可使用第2種變異性測量的方式，稱為標準差。標準差主要是利用離差（deviation）的概念，亦即一個數值和平均數之間的距離，用符號表示為 $X_i-\overline{X}$ ，若是正數，代表數值大於平均數；若是負數，代表數值小於平均數。

為了求得平均的分散程度，須先計算離差的總和，再除以數值的總個數。但因為有些數值的離差大於0，而有些數值的離差小於0，在正負相抵之下，離差的總和等於0，此點也是平均數的一個重要特質。

(1) $\begin{equation*}\sum_{i=1}^{n} (X_i-\overline{X})=0\end{equation*}$

由於離差的總和為0，便無法計算出平均離差。為了解決該問題，可將每一個離差平方後，再將其加總，這些加總後的離差平方，即稱為離差平方和（sum of squared deviations）或簡稱為平方和（sum of squares），簡寫為 $SS$ 。

(2) $\begin{equation*}SS=\sum_{i=1}^{n} (X_i-\overline{X})^2\end{equation*}$

理論上，將離差平方和除以數值的總個數 $N$ 後，即為平均離差平方和。但為了使樣本的標準差能夠更正確地估計母群體的標準差，因此在計算樣本的標準差時，通常會將離差平方和除以 $N-1$ ，而不是 $N$ 。

(3) $\begin{equation*}\frac{SS}{N-1}=\frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{N-1}\end{equation*}$

透過上述的過程，得到平均離差「平方和」，但平方的概念增加了解釋上的困難。因此，最後一個步驟即是去平方，讓平均離差平方和變成平均離差，和原本數據資料的單位一致，而這個平均離差就是所謂的標準差，符號為 $s$ 。

(4) $\begin{equation*}s=\sqrt{\frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{N-1}}\end{equation*}$

現在以上面的11個數值為例子，練習標準差的計算。首先，計算出這11個數值的平均數：

$\overline{X}=\frac{12+15+22+29+32+40+53+58+67+74+82}{11}=44$

然後計算出每一個數值和平均數間的離差 $(X_i-\overline{X})$ ，再將每一個離差平方 $(X_i-\overline{X})^2$ 。最後，加總所有的離差平方，得到離差平方和 $5884$ （見下表）。

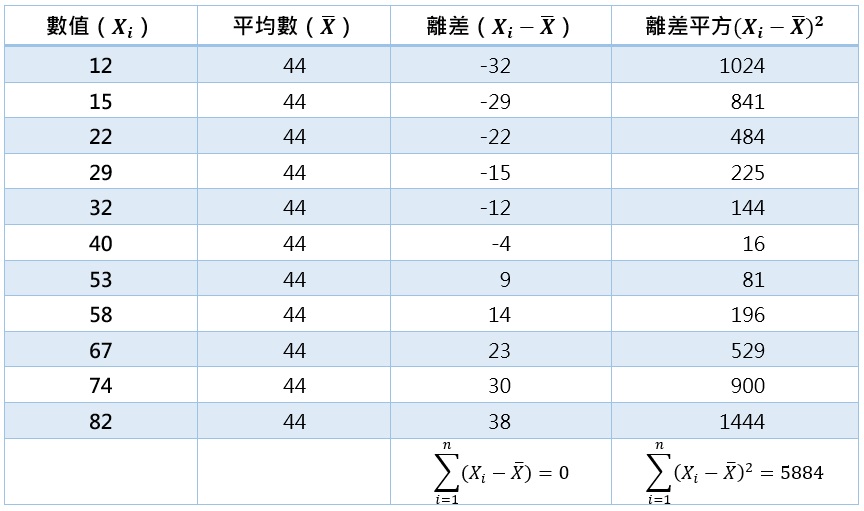
將離差平方和帶入上述的公式(4)，即可計算出標準差：

$s = \sqrt{\frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{N-1}} = \sqrt{\frac{5884}{11-1}} \approx 24.257$

標準差是一個相對於平均數的分散程度之測量方式，使用了資料裡的所有數值，小的標準差代表資料離平均數較近，大的標準差代表資料離平均數較遠。此外，標準差和平均數一樣，不容易受到抽樣變異的影響。換句話說，當從一母群體裡連續地抽出數個樣本，每一個樣本皆可算出全距和標準差，此時標準差在樣本間的數值變異會遠小於全距，而這也是標準差較常被使用的原因。

變異數

第3種變異性測量的方法為變異數，即是平均離差平方和，也就是上述的公式(3)，符號為 $s^2$ 。但是變異數使用「平方」的概念，解釋上較困難，因此很少在描述統計裡使用，而較常出現在推論統計裡。

$s^2 = \frac{SS}{N-1}=\frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{N-1}$

以上面的11個數值為例，變異數為：

$s^2 = \frac{SS}{N-1} = \frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{N-1} = \frac{5884}{11-1} = 588.4$

瞭解了資料的變異性測量之3種方法後，接下來探討如何運用SPSS或Excel來找到這3種變異性測量的統計量。

運用SPSS取得變異性測量的統計量

將上述的11個數值輸入至SPSS的資料編輯器中，變項名稱設為SCORE，接著點選功能表的分析 » 敘述統計 » 次數分配表，帶出「次數分配表」視窗。關於SPSS資料輸入的方法，請參考SPSS操作環境和資料輸入。

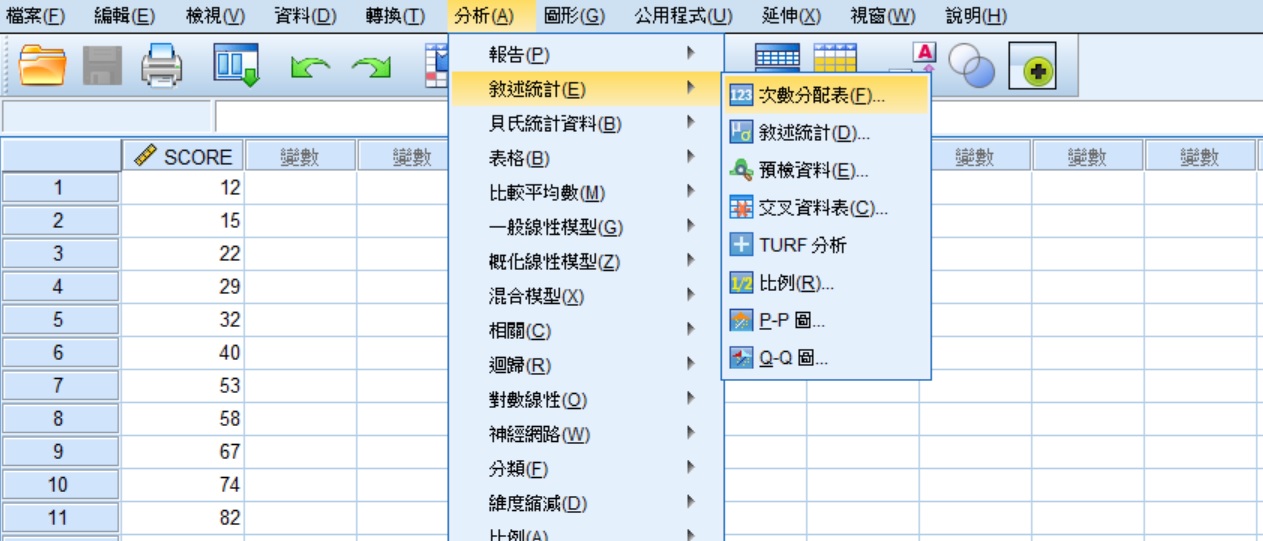
在「次數分配表」視窗裡，將變項SCORE從左邊的方框移至右方的變數(V)方框中，接著點選最右邊的統計資料(S)鈕，帶出「次數：統計量」視窗。

在「次數：統計量」視窗裡，勾選百分位值方框裡的四分位數(Q)和離差方框裡的標準差(T)、變異(V)和範圍(N)，也可勾選最小值(I)和最大值(X)，按下最下方的繼續(C)。回到「次數分配表」視窗後，再按下確定。

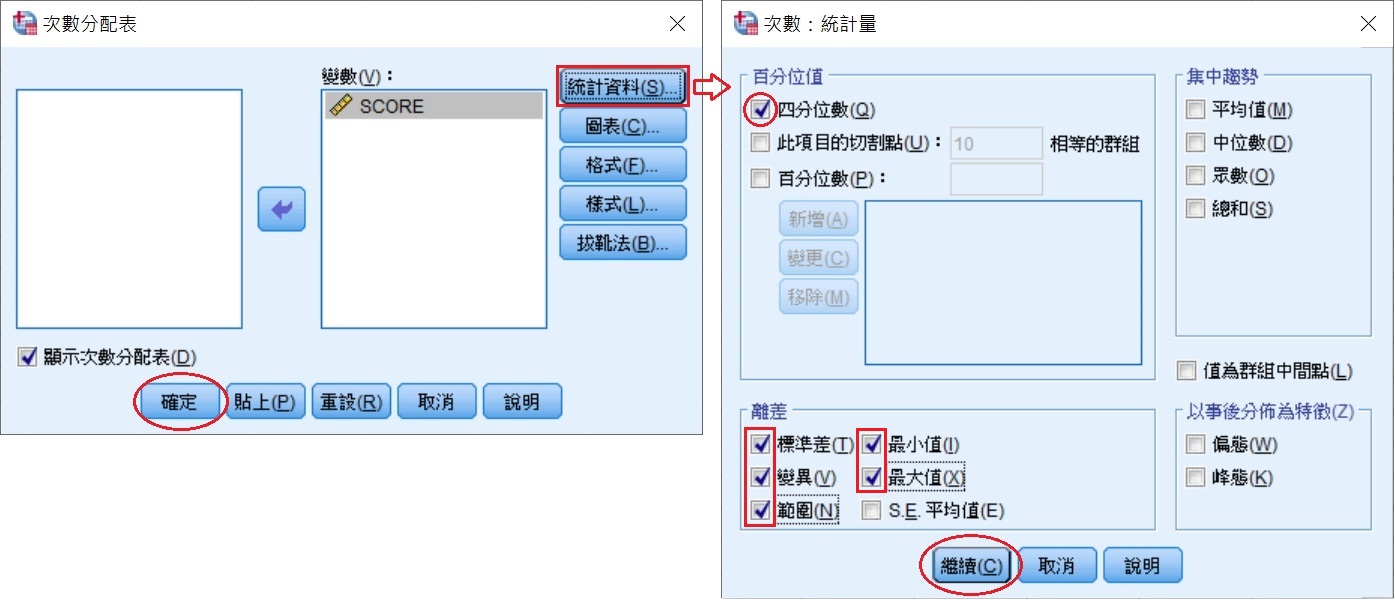
dialog box of measures of variability in spss

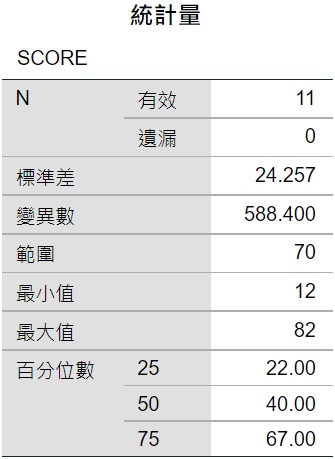
SPSS會輸出如下的統計量表。從該表可以看出，資料裡一共有11個數值，最小值為12，最大值為82，「範圍」即是全距（最大值減最小值），為70。第50百分位數，也就是中位數，為40。四分位距為第75百分位數（67）減第25百分位數（22），結果為45。這11個數值的標準差為24.257，變異數為588.4。所有的運算結果皆與上面紙筆計算的結果相同。

若沒有SPSS，也可以使用Excel來計算變異性測量的3個統計量，而且使用上很簡單，以下來示範操作方法。

運用Excel取得變異性測量的統計量

SPSS有圖形化的操作介面，使用者用滑鼠點選即可進行大多數的分析，但使用Excel執行統計分析時則須在儲存格裡輸入函數或運算公式才可。有一點須注意的是，在Excel的儲存格裡輸入任一函數或運算前，須先輸入等於的符號（＝），再輸入函數或運算公式。以下示範利用Excel的函數來取得全距、四分位距、標準差和變異數的方式。

最小值、最大值和全距

在一空白的活頁簿中，輸入上述的11個數值，然後找3個空白的儲存格，輸入「最小值」、「最大值」和「全距」。

利用MIN函數求得最小值，語法為：MIN(number1, [number2], …)。括弧內為資料的範圍，可逐一輸入數值或明確地指出資料的儲存格範圍。這裡我們使用後者，在「最小值」右邊的儲存格裡輸入=MIN(A1:A11)，輸入完成後按下Enter，傳回數值12，此即為最小值。

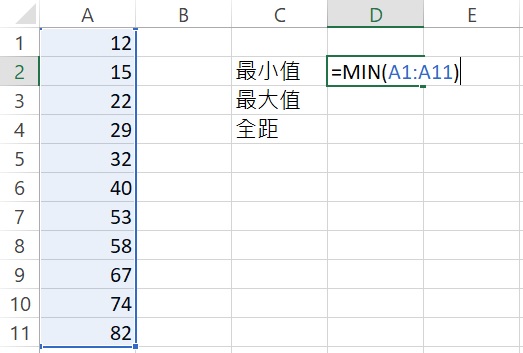
再利用MAX函數找到最大值，語法為：MAX(number1, [number2], …)。括弧內為資料的範圍，可逐一輸入數值或明確地指出資料的儲存格範圍。這裡我們使用後者，在「最大值」右邊的儲存格裡輸入=MAX(A1:A11)，輸入完成後按下Enter，傳回數值82，此即為最大值。

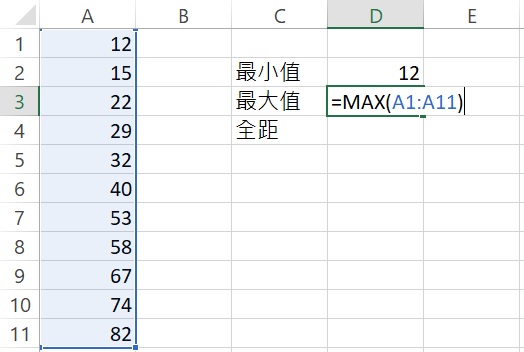
最後，因為全距是最大值（儲存格D3）減最小值（儲存格D2），所以在「全距」右邊的儲存格裡輸入=D3-D2，輸入完成後按下Enter，傳回數值70，此即為全距。

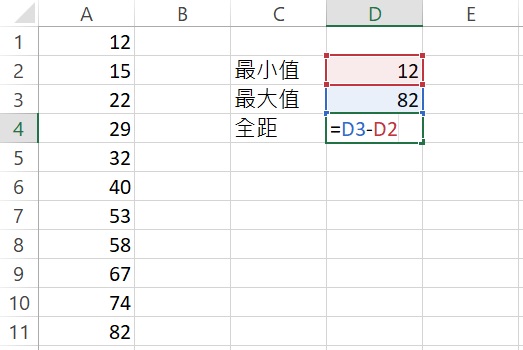
透過上面的步驟，即可求得資料裡的最小值、最大值和全距。

四分位距

在數值所在的A欄旁邊找4個空白的儲存格，依序輸入「第1四分位數」、「第2四分位數」、「第3四分位數」和「四分位距」。Excel計算四分位數的函數因演算法的不同而區分為QUARTILE.INC和QUARTILE.EXC，由於QUARTILE.EXC和SPSS採用相同的演算法，所以這裡使用該函數。

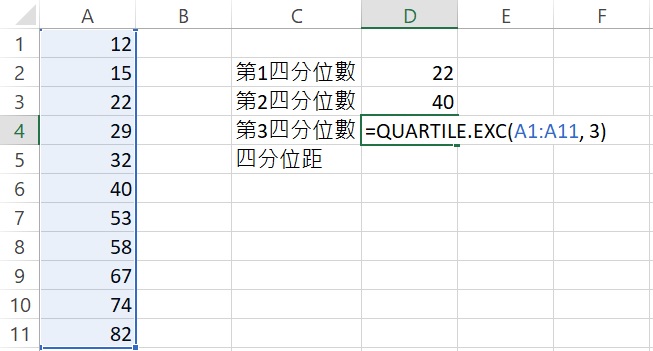
QUARTILE.EXC函數語法為：QUARTILE.EXC(array, quart)，括弧內須指出資料的儲存格範圍和欲求得的四分位數。因為此處要先找第一四分位數，所以在「第1四分位數」右邊的儲存格裡輸入=QUARTILE.EXC(A1:A11, 1)，輸入完成後按下Enter，傳回數值22，此即為第一四分位數。

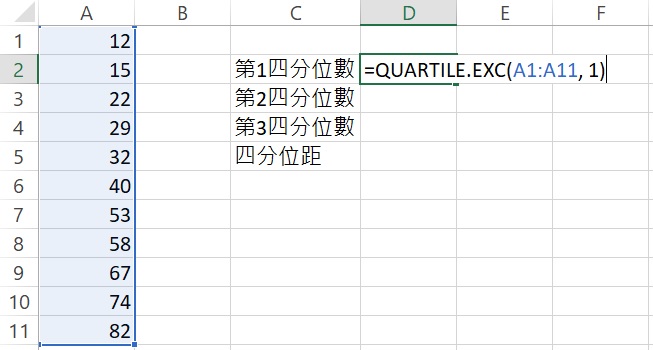
雖然計算四分位距不需要第二四分位數，但可當作練習。在「第2四分位數」右邊的儲存格裡輸入=QUARTILE.EXC(A1:A11, 2)，輸入完成後按下Enter，傳回數值40，此即為中位數。

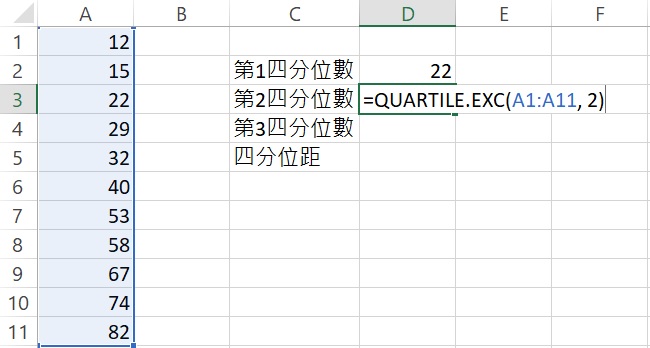
接著，找第三四分位數。在「第3四分位數」右邊的儲存格裡輸入=QUARTILE.EXC(A1:A11, 3)，輸入完成後按下Enter，傳回數值67，此即為第三四分位數。

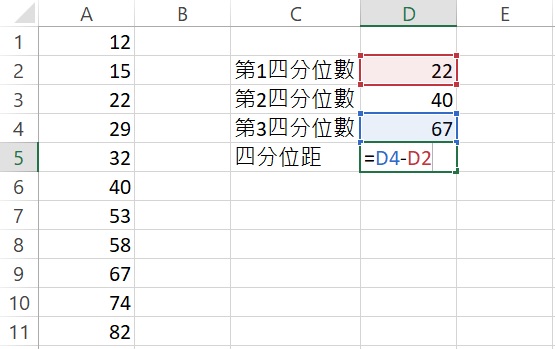
最後，因為四分位距為第三四分位數（儲存格D4）減第一四分位數（儲存格D2），所以在「四分位距」右邊的儲存格裡輸入=D4-D2，按下Enter後，傳回數值45，此即為四分位距。

經過上述的步驟，即可求得資料裡的第一四分位數、第二四分位數、第三四分位數和四分位距。

標準差和變異數

在數值所在的A欄旁找2個空白儲存格，依序輸入「標準差」和「變異數」。計算標準差的函數為STDEV.S，語法為：STDEV.S(number1, [number2], …)，括弧裡為資料的範圍，可逐一輸入數值或明確指出資料的儲存格範圍。

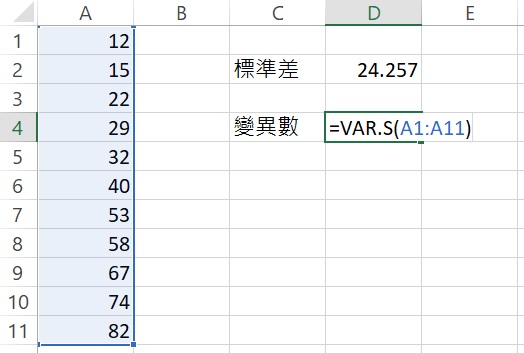
在「標準差」右邊的儲存格裡輸入=STDEV.S(A1:A11)，該語法要求Excel計算儲存格A1到A11的標準差，輸入完成後按下Enter，傳回數值24.257，即為標準差。

計算變異數的函數為VAR.S，語法為：VAR.S(number1, [number2], …)。在「變異數」右邊的儲存格裡輸入=VAR.S(A1:A11)，要求Excel計算儲存格A1到A11的變異數，輸入完成後按下Enter，傳回數值588.4，此即為變異數。

Excel還有兩個和STDEV.S和VAR.S函數相當類似的函數，分別為STDEV.P和VAR.P函數，他們之間的差別在於，STDEV.S和VAR.S函數用在樣本的標準差和變異數的計算上，而STDEV.P和VAR.P函數則用在母群體的標準差和變異數的計算上。因為範例的11個數值為樣本資料，所以這裡我們使用STDEV.S和VAR.S函數。

從上面的軟體操作示範過程可以知道，不論是使用SPSS或Excel，都可以計算出全距、四分位距、標準差和變異數等測量分散程度的統計量。只是使用SPSS時，可在單一的視窗中，一次勾選所有想要的變異性測量的統計量，不像Excel須利用不同的函數來計算，所以使用上SPSS顯得較方便與快速。

以上為本篇文章對於變異性測量的介紹，希望透過本篇文章，您瞭解了全距、標準差和變異數的意義和計算方法，也學會了如何使用SPSS和Excel去取得這些統計量。

若您喜歡本篇文章或想學習更多社會統計的知識和軟體操作，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站喔！另外，也歡迎您按讚和追蹤我們的Facebook和Twitter專頁喲！