皮爾森積差相關係數（Pearson product-moment correlation coefficient）是相關係數的一種，用來測量成對的兩個變項裡，當其中一個變項數值變化的時候，另一個變項往相同或相反方向變化的程度。簡單來說，是測量兩變項間關係的方向和強度的一個量化數值。
為了不讓變項間不同的測量尺度和單位影響相關係數的計算，皮爾森積差相關係數先將變項標準化，轉換成單位相同的標準分數後，再計算其間的關聯性。更詳盡的相關概念和皮爾森積差相關係數意義的介紹，請參考何謂皮爾森積差相關係數。
計算皮爾森積差相關係數的方式有傳統的紙筆計算和電腦軟體的使用，雖然紙筆計算須耗費相當多的時間，而且只適合總個數很少的樣本，但不失為一個瞭解皮爾森積差相關係數來源的過程。下面將先舉一個例子，然後介紹3種計算方法。若您只對其中的一種計算方法感興趣，也可點選下面的連結，即可直接跳至您想瞭解的內容。
皮爾森積差相關係數的例子
假設有一位老師想探討學生期中考成績和期末考成績之間的關聯性，她隨機抽取出10位修課的學生，他們的期中考（MIDTERM）和期末考成績（FINAL）如下表所示。試問這10位學生的期中考和期末考成績之間的關聯程度是多少？
先繪製一散布圖，觀察MIDTERM和FINAL兩變項之間的關係，如下圖。從散布圖可以看出，雖然成對的兩變項所構成的點略為分散，但仍舊可看出兩變項呈現正向、不完全的線性關係。
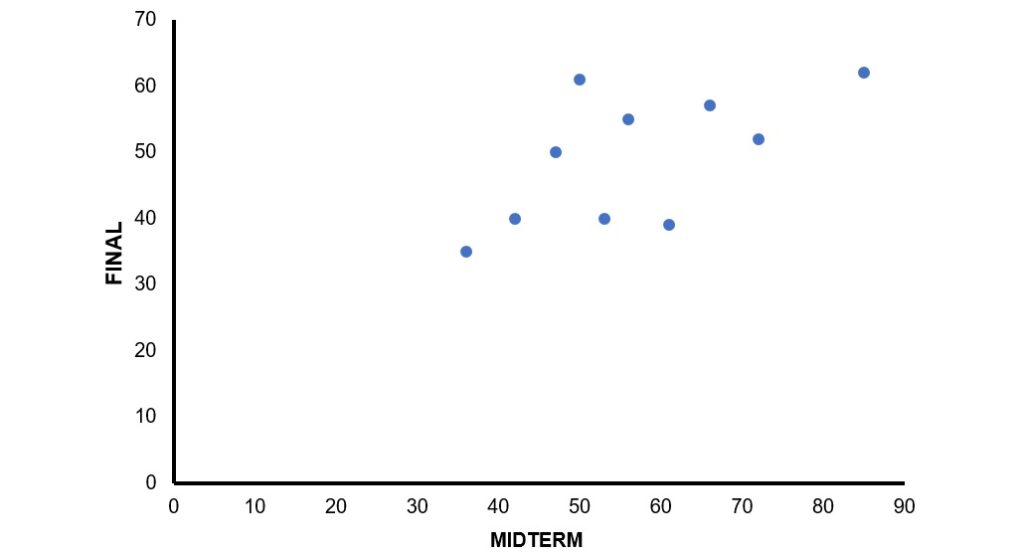
以下將使用這10位學生的資料，示範紙筆計算、利用SPSS和Excel等3種求得皮爾森積差相關係數的方法。
紙筆計算皮爾森積差相關係數
皮爾森積差相關係數是將兩個變項的數值皆轉換成標準分數後，再計算其間關聯性的一個量化數值。運用此概念，讓
為成對的X和Y變項標準分數的交叉乘積和、
為配對的X和Y變項的總組數，皮爾森積差相關係數的公式如下：
![\[ r=\frac {\sum z_x z_y}{N-1} \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-99c81998d75af9a7e5f94765176daf24_l3.png "Rendered by QuickLaTeX.com")
此外，皮爾森積差相關係數也是兩個變項的共變異數（covariance）除以兩變項的標準差乘積而得到的數值，可被視為標準化的共變異數，公式如下：
![\[ r=\frac {cov_{xy}}{s_x s_y}=\frac {\sum (x_i-\overline x)(y_i-\overline y)}{(N-1)s_x s_y} \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-179170a483029b0ea3c838c07664f913_l3.png "Rendered by QuickLaTeX.com")
因為上面的兩個公式皆須先計算兩變項各自的平均數、標準差，再計算兩變項各個數值的離差，整個過程可能充斥著小數點的運算，很容易造成計算錯誤或進位誤差，所以可改使用下面的運算公式來計算：
(1) ![\begin{equation*}r=\frac {\sum xy-\dfrac {(\sum x)(\sum y)}{N}}{\sqrt {{ \left [ \sum x^2-\dfrac{(\sum x)^2}{N} \right ]}{ \left [\sum y^2-\dfrac {(\sum y)^2}{N} \right ]}}}\end{equation*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-1161b91b7c50e205f6234c5d6ab764e7_l3.png "Rendered by QuickLaTeX.com")
上面的公式(1)只須使用到原始分數，不需要事先計算出平均數、標準差和離差等數值，運算過程中比較不容易出錯。在套用公式(1)前，先把需要的數值在如下的表格裡計算出來：
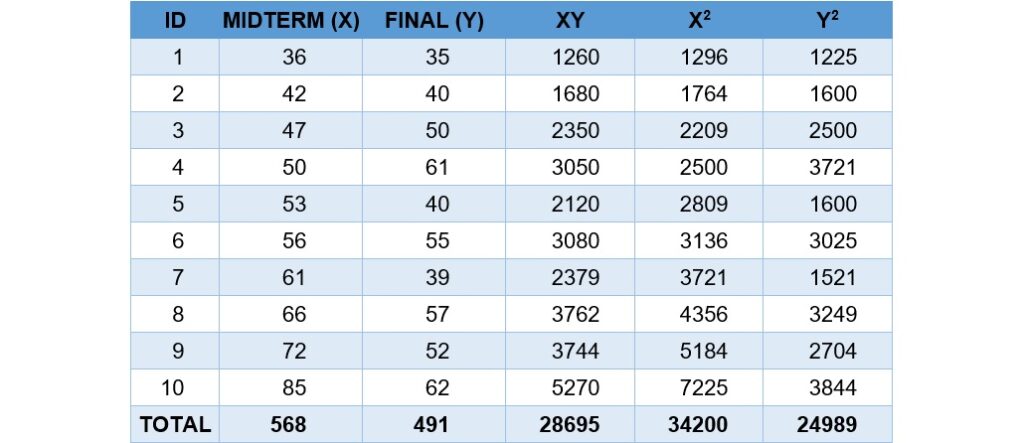
接著，把利用上面表格計算得到的
、
、
、
和
數值帶入上面的公式(1)中。如果您不熟悉數學符號和總和運算，請參考社會統計常用的基本數學符號和運算。
![\begin{align*}r &=\frac {28695-\dfrac{568\times 491}{10}}{\sqrt{ \left [ 34200-\dfrac{(568)^2}{10} \right ] \left [ 24989-\dfrac{(491)^2}{10} \right ]}} \\[5pt]&=\frac {28695-27888.8}{\sqrt{1937.6 \times 880.9}} \\[5pt]&=\frac {806.2}{1306.457745} \\[5pt]&\approx 0.617\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-2f08ac088a96961737fa81ba18f3910b_l3.png "Rendered by QuickLaTeX.com")
從計算結果得知，學生的期中考和期末考成績的皮爾森積差相關係數為0.617。數值為正數，代表兩變項之間為正向關係，也就是期中考的成績愈高，期末考的成績也愈高。
不過皮爾森積差相關係數並非母群體相關係數的不偏誤估計值，尤其是在樣本數很小的時候，樣本相關係數無法準確地估計母群體相關係數，此時可改計算調整後相關係數。雖然樣本數較大時，調整前、後的相關係數不會相距太遠，但當樣本數很小的情況下，調整後相關係數是個相對無偏誤的母群體相關係數估計值。關於調整後相關係數的詳細說明，請參考調整後相關係數的意義和計算。
運用 SPSS 計算皮爾森積差相關係數
將上面例子裡兩變項的數值輸入至SPSS資料編輯器中，再點選功能表的分析 » 相關 » 雙變異數，開啟「雙變量相關性」視窗。關於SPSS資料輸入的方法，請參考SPSS操作環境和資料輸入。
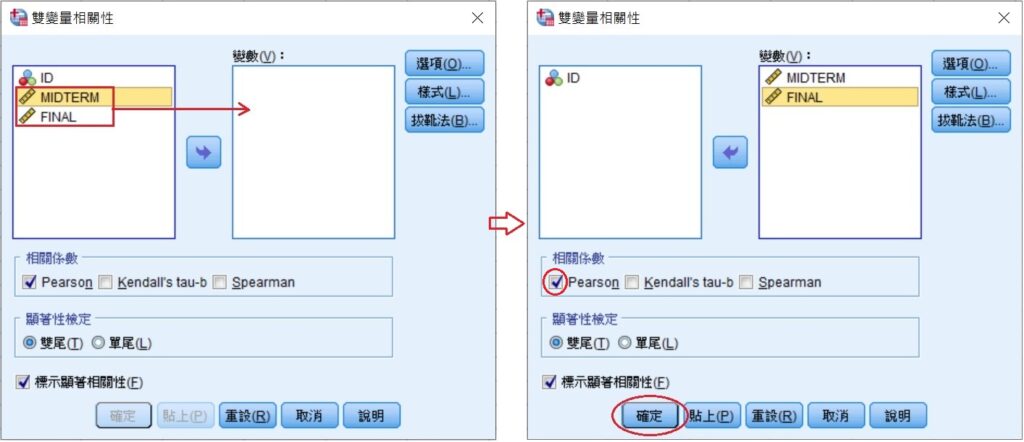
在「雙變量相關性」視窗中，將MIDTERM和FINAL兩變項移至變數(V)方框中，確定相關係數長方框中的Pearson選項有被勾選，其餘的設定不動，按下視窗最下方的確定。
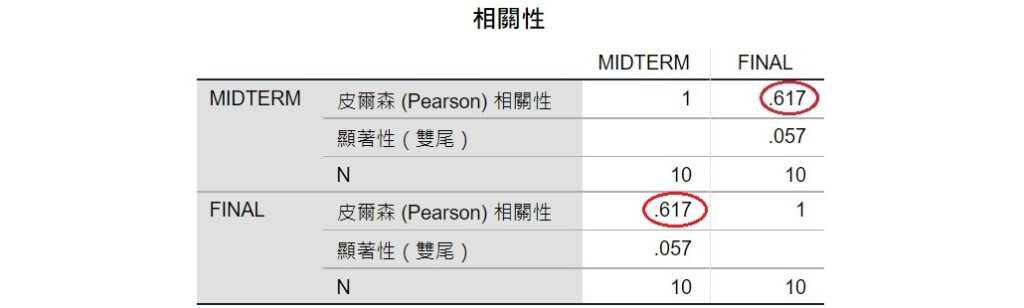
經過上面的步驟，SPSS會輸出如下的皮爾森積差相關係數的表格。不論要看MIDTERM欄或FINAL欄都可以，相關係數的數值為0.617，與上面紙筆計算的結果相同。
若您沒有SPSS或其他統計分析軟體，也可以使用微軟的Excel來求得皮爾森積差相關係數，而且操作上相當簡單，下面示範Excel的操作方式。
運用 Excel 計算皮爾森積差相關係數
將上面例子裡兩變項的資料輸入至Excel的空白活頁簿或工作表中，或利用SPSS的匯出功能將資料轉換成Excel可開啟的資料檔。關於SPSS的匯出功能，請參考〈匯出SPSS資料至Excel並繪製盒形圖〉裡的匯出SPSS資料至Excel。
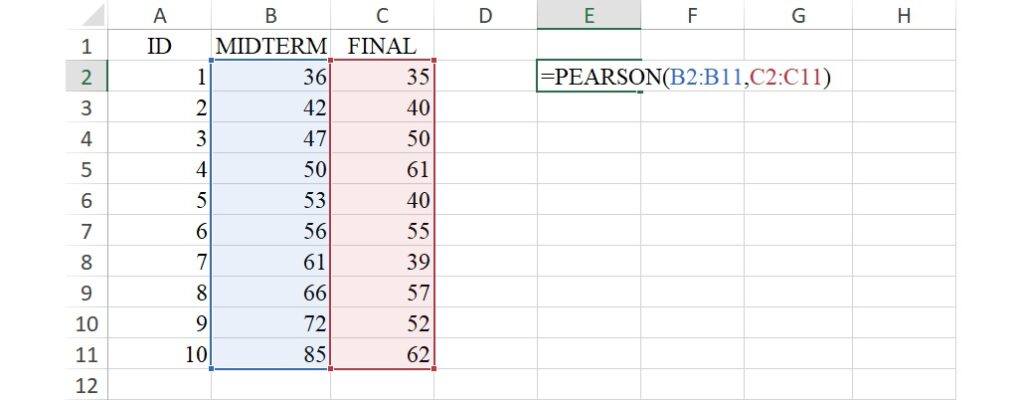
Excel計算皮爾森積差相關係數的函數為PEARSON 函數，語法為PEARSON(array1, array2)，括弧裡兩個引數的意義分別為：
- array1：X 變項或自變項的資料儲存格範圍。
- array2：Y 變項或依變項的資料儲存格範圍。
在例子裡X變項的資料儲存格範圍是B2到B11，Y變項的資料儲存格範圍是C2到C11。找任一空白的儲存格，輸入=PEARSON(B2:B11, C2:C11)。完成後，按下Enter，傳回數值0.617，此即皮爾森積差相關係數。
除了PEARSON函數之外，Excel裡的CORREL函數和資料分析工具裡的相關分析都可以用來取得皮爾森積差相關係數。若您想更深入瞭解這些功能的操作方法，可以參考如何使用Excel取得皮爾森積差相關係數。
不論是紙筆計算或使用SPSS、Excel等軟體，皆可計算出皮爾森積差相關係數。雖然紙筆計算的過程可以讓人瞭解皮爾森積差相關係數的意義，但在資料龐大的時候，就會變得不切實際，此時SPSS或Excel反而是更為合適的方法，且透過幾個簡單的操作步驟即可求得相關係數的數值。
求得皮爾森積差相關係數後，若想進一步探討兩變項間的關係是否真實地存在於母群體中，則須透過假設檢定來瞭解，這部分的內容請參考皮爾森積差相關係數的假設檢定。
以上為本篇文章對皮爾森積差相關係數計算方法的介紹，希望透過本篇文章，您學會了紙筆計算、利用SPSS和Excel計算皮爾森積差相關係數的方法。若您喜歡本篇文章，請將本網站加入書籤，並持續回訪本網站喔！另外，也歡迎您追蹤本網站的Facebook和／或X（Twitter）專頁喲！
如果您覺得本篇文章對您有幫助，歡迎買杯珍奶給 Dr. Fish！小小珍奶，大大鼓勵，您的支持將給Dr. Fish更多撰寫優質文章的動力喔！
