研究執行的過程中，當原始資料蒐集完成後，便要開始進行資料整理與分析。統計分析最主要可分為兩個部分：描述統計（descriptive statistics）和推論統計（inferential statistics），雖然兩者皆是利用資料進行分析，但採用的分析方法和想達到的目的並不相同，以下分別說明。
描述統計
描述統計是以組織、概括的方式來呈現資料，目的在描述資料的特性，讓人能夠輕易地理解資料所傳達的訊息。因為剛蒐集完成的資料表面上看起來只是一堆雜亂的數字，很難看出端倪，此時就可用描述統計來瞭解資料的整體樣貌。
舉個例子來說，看看下面的兩組分數。若不使用任何紙筆工具，只靠肉眼觀察的情況下，能否說出這兩組分數是否相似呢？是否不同呢？若是不同，差別在哪裡呢？
事實上，只靠觀察很難看出上面兩組分數之間的差別。但若用圖形來呈現上面兩組分數的分布狀態，則可以輕易地看出兩者之間的差異。從下圖可看出，左邊那一組的分數呈現常態分配，而右邊那一組分數則為正偏態的分布型態。
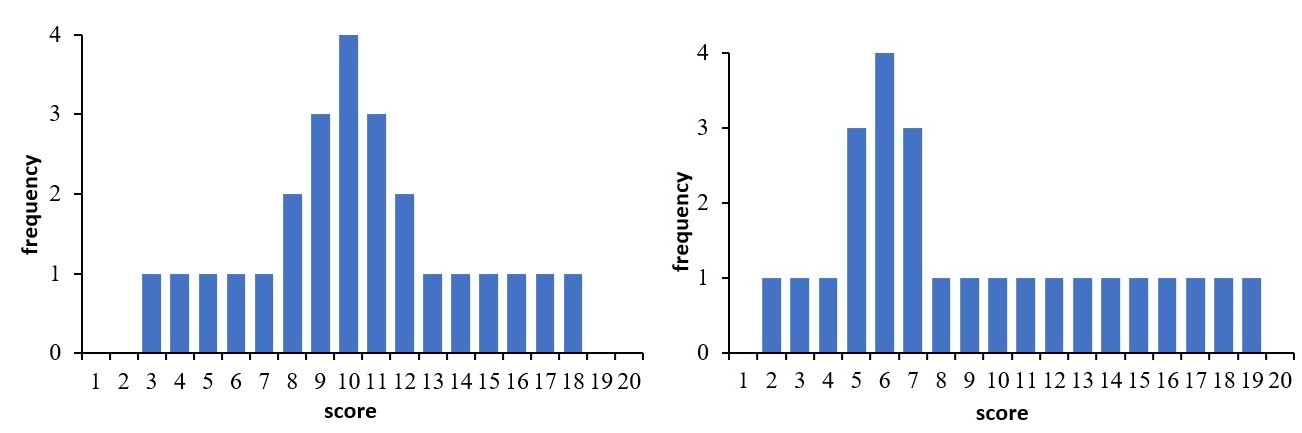
上述利用圖形的繪製來顯示資料的分布型態即是描述統計的一種。此外，眾數、中位數和平均數等集中趨勢的測量，全距、標準差和變異數等變異性的測量，因為這些測量的目的都在描述資料的特性，所以全部屬於描述統計的範疇。
因此，描述統計的重要功能即在於使用量化或圖形的方式來描述、概括資料，讓人更容易理解資料的特性和全貌。除此之外，描述資料特性的統計程序是一套廣受認可的標準化程序，不但能減少研究人員憑藉個人想法去揣測資料特性的可能性，還可讓資料的解釋變得更客觀和容易理解。
推論統計
推論統計是將樣本資料推論至母群體的統計技術，可能為母體參數的估計或自變項和依變項之間是否存在系統性的關聯，通常會牽涉到機率和各種的統計檢定方法，例如單一樣本ｔ檢定、變異數分析、皮爾森積差相關係數的假設檢定。
舉例來說，假設有一位教師想瞭解在他任教國中的一年級新生的智商，由於新生的人數很多，若要對每一位學生進行測量將會花費許多的時間和金錢，因此他隨機抽取出100位新生並給他們智力測驗。透過這樣的過程，因為100位新生是能夠代表所有新生的隨機樣本，所以可用這100位學生的資料來估計該校所有新生的智商。
在蒐集到100位新生的智力測驗分數後，這位老師可使用單一樣本ｔ檢定來估計母體參數（也就是全部新生的智商）可能存在的範圍，稱為信賴區間，然後做出類似「有0.95的機率或95%的信心程度，國一新生的智商落在65到75之間」的結論。
因此，推論統計的主要功能不在於描述資料的特性，而是利用樣本資料進行運算，並將運算結果推論至母群體上。此外，由於推論統計立基於機率論，所以研究結論屬於試驗的性質而不是絕對的真理，而這也是為什麼在撰寫研究發現的時候，通常會使用「得到這個研究結果的機率小於0.05或0.01」的措詞。
以上為描述統計和推論統計之間差別的說明，希望對您有幫助。關於描述統計和推論統計各別涵蓋的分析技術，將會在本網站的其他文章裡進行介紹喔。
若您喜歡本篇文章，請將本網站加入書籤，作為您的學習工具，並持續回訪本網站。此外，也歡迎您追蹤我們的Facebook和Twitter專頁喔！
