🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
社會統計常用的基本數學符號和運算
基礎社會統計所使用的數學很簡單,大多為加減乘除的運算,雖然有時會看到較複雜的公式,例如皮爾森積差相關係數的計算、各種統計檢定的檢定統計量,但若能釐清算術運算的順序,應該都能迎刃而解。
不過,對於不喜歡數學的社會科學領域的學生或許久未接觸數學的人士,即使是簡易的運算,也可能變得生疏。因此,為了讓本網站的社會統計相關的內容更易於理解,本篇文章將回顧一下社會統計常用的基本數學符號和運算。
雖然電子計算機的使用已經普及,且大多數的社會統計課程也允許電子計算機的使用,藉此降低運算錯誤的機率,但其使用仍舊建立於數學基礎上,所以具備基礎數學的概念將有助於使用正確的程序來進行運算。以下將簡單地複習基本的數學符號和算術運算的規則。
數學符號
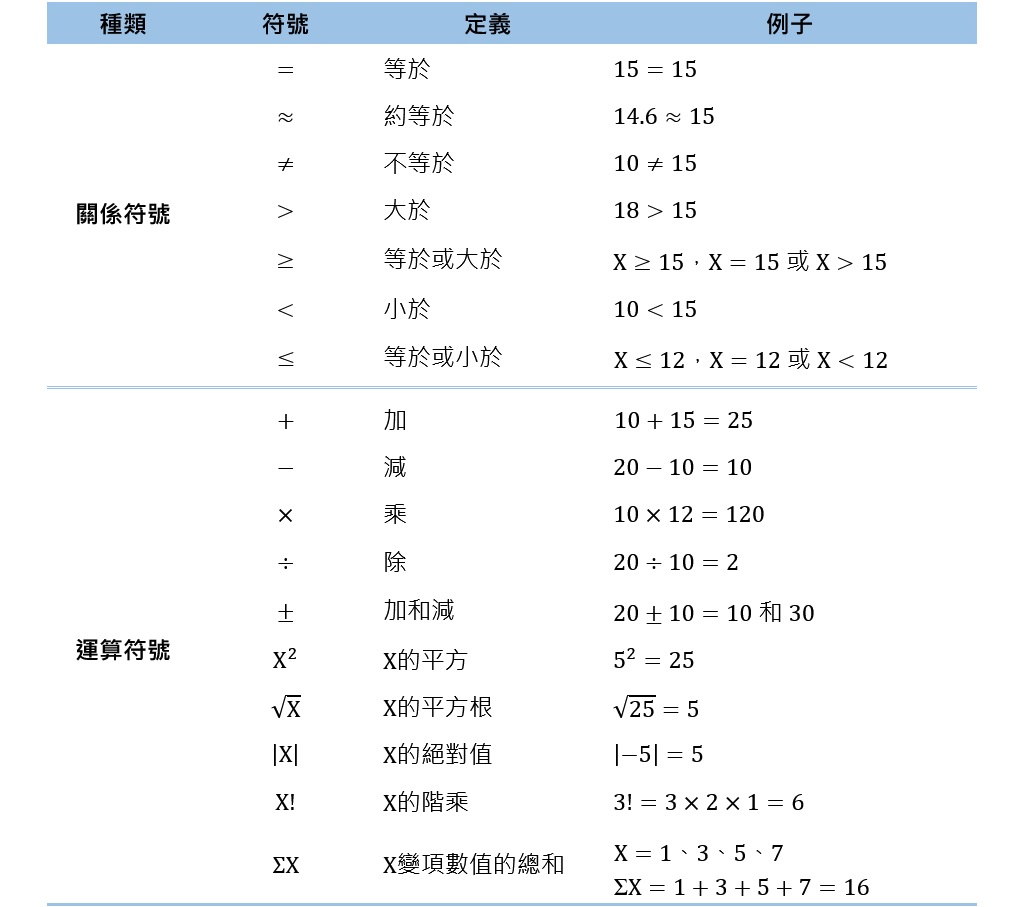
基本的數學符號包括關係符號(relation symbol)和運算符號(operation symbol)。關係符號用來表示相等或比較,例如=、>、<;運算符號則用於數值的計算,例如+、-、×、÷,下表為社會統計常用的數學符號。
總和/求和運算
總和或求和(summation)是社會統計最常使用到的運算方法,指將一組數值的全部或部分分數相加,通常會用希臘符號Σ(讀音為sigma)來表示。總和運算的代數呈現方式如下:
(1) ![]()
總和運算符號Σ的下方指出第1個要加總的分數,符號的上方則指出最後一個要加總的分數,所以上面的公式是指把第1個分數加到第![]() 個分數。
個分數。
若計算時要將所有的數值相加,也就是從第1個分數加到第![]() 個分數,則通常會省略總和運算符號的上、下限標示,也會省略
個分數,則通常會省略總和運算符號的上、下限標示,也會省略![]() 的下標,變成
的下標,變成![]() 。
。
另外有兩個和上面的方程式(1)很類似,而且也是社會統計很常使用到的總和運算,就是![]() 和
和![]() 。
。![]() 是指每一個分數平方後再相加,方程式如下:
是指每一個分數平方後再相加,方程式如下:
(2) ![]()
不同於![]() 的每個分數平方後再相加,
的每個分數平方後再相加,![]() 是指全部的分數相加後再整個平方,方程式為:
是指全部的分數相加後再整個平方,方程式為:
(3) 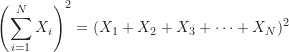
和方程式(1)一樣,若計算的過程是加總一組數值裡的每一個分數,則總和符號的上、下限標示和![]() 的下標皆可省略,直接寫成
的下標皆可省略,直接寫成![]() 和
和![]() 。雖然這3個總和運算的方程式看起來很類似,但實際上他們的計算結果完全不同,以下舉個例子來練習。
。雖然這3個總和運算的方程式看起來很類似,但實際上他們的計算結果完全不同,以下舉個例子來練習。
✎練習題
假設![]() 變項有5個分數,從小至大分別為2、8、12、15、20,試問
變項有5個分數,從小至大分別為2、8、12、15、20,試問![]() 、
、![]() 和
和![]() 分別為多少?
分別為多少?
![]() 變項有5個分數,
變項有5個分數,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,套用上面的方程式(1)、(2)和(3),
,套用上面的方程式(1)、(2)和(3),![]() 、
、![]() 和
和![]() 的計算過程如下:
的計算過程如下:
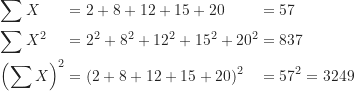
從這練習題可以知道,![]() 。因為社會統計的公式很常使用到這3種總和運算,例如標準差、皮爾森積差相關係數,所以釐清他們之間的不同很重要。
。因為社會統計的公式很常使用到這3種總和運算,例如標準差、皮爾森積差相關係數,所以釐清他們之間的不同很重要。
加法和減法
進行加法(addition)運算時,數值的順序不會影響計算的結果,例如![]() 。但相加的數值裡若有負數的時候,須注意運算符號的變化。
。但相加的數值裡若有負數的時候,須注意運算符號的變化。
![]()
和加法運算不同,進行減法(subtraction)運算的時候,數值的順序不能隨意更動,否則會影響計算的結果,例如![]() 。另外,相減的數值裡若有負數的時候,須注意運算符號的變化。
。另外,相減的數值裡若有負數的時候,須注意運算符號的變化。
![]()
乘法
進行乘法(multiplication)運算的時候,數值的排列順序不會影響計算的結果,例如:
![]()
一組數值相乘的時候,若數值裡的負數個數為偶數,相乘的結果為正數;若數值裡的負數個數為單數,則相乘的結果為負數。
![]()
當乘法和加法或減法一起使用的時候,須先進行乘法後再進行加法或減法。但若有括號存在的時候,則須先執行括號裡的運算。
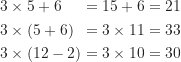
若括號被包含在中括號內,須先進行括號內的運算,再執行中括號裡的運算,最後再進行所有括號外的運算。例如:
![Rendered by QuickLaTeX.com \begin{align*}[ 3 \times (2+7)+5 ] \times 10 &= [ 3 \times 9+5 ] \times 10 \\&= [ 27+5 ] \times 10 \\&= 32 \times 10 \\&= 320\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-5c752d2be7353abfefd33e4c16513b3d_l3.png)
若相乘的數值帶有小數點,須注意小數點所在的位置,避免計算結果放錯小數點的位置。例如:
![]()
除法
進行除法(division)運算時,數值的位置不能夠隨意變換,例如![]() 。除了使用÷來表示除法運算外,還可以使用下面的方式來呈現:
。除了使用÷來表示除法運算外,還可以使用下面的方式來呈現:
![]()
橫線下方的數值稱為分母(denominator),橫線上方的數值稱為分子(numerator)。以上面的例子來看,分母為5,分子為10,而這也是社會統計的公式很常使用的呈現方法。
一組數值相除的時候,若負數的個數為偶數,計算的結果為正數;若負數的個數為單數,則計算的結果為負數。
![]()
若除法和加法或減法一起使用的時候,須先進行除法後再進行加法或減法。但若有括號存在的時候,須先進行括號內的運算。
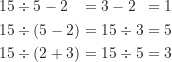
若括號被包含在中括號內,須先進行括號內的運算,再執行中括號內的運算,最後再進行所有括號外的運算。
![Rendered by QuickLaTeX.com \begin{align*}30 \div [(5-2) \times (2+3)] &= 30 \div [3 \times 5] \\&= 30 \div 15 \\&= 2\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-b2b7d42a55640cd1067b73a8811c8748_l3.png)
若相除的數值帶有小數點,須注意小數點所在的位置,避免計算結果放錯小數點的位置。例如:
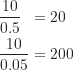
指數和平方根
指數(exponentiation)是指一個數值的幾次方,可用符號![]() 來表示。
來表示。![]() 稱為底數,
稱為底數,![]() 即為指數,白話來說就是幾次方,計算方法是將數值
即為指數,白話來說就是幾次方,計算方法是將數值![]() 乘以自己
乘以自己![]() 次。最常見的指數為平方,也就是數值乘以自己2次,例如
次。最常見的指數為平方,也就是數值乘以自己2次,例如![]() 。再舉兩個例子:
。再舉兩個例子:
![]()
若將兩個具有相同底數的指數相乘,則底數維持不變,指數為兩個指數相加。例如:
![]()
若將兩個具有相同底數的指數相除,則底數維持不變,指數為兩個指數相減(或分子的指數減分母的指數)。例如:
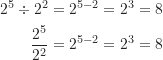
平方根(square root)為平方的相反。假設![]() ,
,![]() 稱為
稱為![]() 的平方,
的平方,![]() 則稱為
則稱為![]() 的平方根,也就是
的平方根,也就是![]() 。例如:
。例如:
![]()
絕對值
絕對值(absolute value)會用兩條垂直的線來表示,例如![]() 的絕對值為
的絕對值為![]() 。絕對值將一個數值轉換為正數,所以正數的絕對值為自己,負數的絕對值則會變成沒有負號的正數。例如:
。絕對值將一個數值轉換為正數,所以正數的絕對值為自己,負數的絕對值則會變成沒有負號的正數。例如:
![]()
階乘
一個正整數的階乘(factorial)是指等於和小於這個正整數的所有正整數的乘積,會用這個正整數和一個驚嘆號來表示,例如5!指5的階乘、8!指8的階乘。這2個階乘的計算方法分別為:
![]()
也就是說,![]() 階乘就是
階乘就是![]() 。此外,有一個比較特別的是,0階乘等於1。
。此外,有一個比較特別的是,0階乘等於1。
排列
排列(permutation)是用來決定數個人或物有幾種被安排在一起的方法,例如從5位學生裡挑出3位不同課程小老師的所有安排方法。若讓![]() 代表人或物的數目,
代表人或物的數目,![]() 代表一次從
代表一次從![]() 挑出來的人或物數目,
挑出來的人或物數目,![]() 為所有可能的安排方法數目,
為所有可能的安排方法數目,![]() 的公式如下:
的公式如下:
![]()
舉例來說,假設有A、B、C、D四位學生,導師打算從4人當中挑出2位分別擔任法學緒論和犯罪學的小老師,試問有幾種排列的方法?先用土法煉鋼的方式,列出所有可能的排列方法:
| A B | B A | C A | D A |
| A C | B C | C B | D B |
| A D | B D | C D | D C |
一共有12種排列方法,但當資料很多的時候,逐一列出的方法並不可行,所以可利用上面的排列公式。這個例子裡一共有4位學生(![]() )且要從中挑出2位(
)且要從中挑出2位(![]() ),把這2個數值帶入上面的公式,計算過程如下:
),把這2個數值帶入上面的公式,計算過程如下:
![Rendered by QuickLaTeX.com \begin{align*}P_2^4 &= \frac {4!}{(4-2)!} \\[5pt]&= \frac {4 \times 3 \times 2 \times 1}{2 \times 1} \\[5pt]&= 12\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-e25c5ed660fbf2ccd8bf4ca03f76f03f_l3.png)
計算結果指出從4位學生當中挑出2位分別擔任不同課程小老師的排列方法有12種,和土法煉鋼的結果是一樣的。在這個例子裡,排列的順序是有意義、重要的,若不在乎排列的順序,則可利用下面「組合」的方法來計算。
組合
組合(combination)是決定數個人或物有幾種被安排在一起的方法,但不在意被安排的順序,也就是排列的順序不重要,例如A、B和B、A為不同的排列但視為相同的組合。若讓![]() 代表人或物的數目,
代表人或物的數目,![]() 代表一次從
代表一次從![]() 挑出來的人或物數目,
挑出來的人或物數目,![]() 為所有可能的組合數目,
為所有可能的組合數目,![]() 的公式如下:
的公式如下:
![]()
同樣用上面A、B、C、D四位學生的例子,假設導師要從這4位學生中挑出2位來擔任法學緒論和犯罪學的小老師,不在乎誰先被挑出來,試問有幾種組合?先用土法煉鋼的方式,列出所有可能的組合:
| A B | B C |
| A C | B D |
| A D | C D |
利用逐一列出的方法可發現一共有6種組合,若改用上面的組合公式來計算,把![]() 、
、![]() 帶入公式裡,計算過程如下:
帶入公式裡,計算過程如下:
![Rendered by QuickLaTeX.com \begin{align*}C_2^4 &= \frac {4!}{2!(4-2)!} \\[5pt]&= \frac {4 \times 3 \times 2 \times 1}{(2 \times 1)(2 \times 1)} \\[5pt]&= 6\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-9bb36b2d970ff21823d9bf75fe94ec6c_l3.png)
利用組合公式計算得到的結果指出,從4位學生中挑出2位學生來擔任2門課程的小老師,若不在乎學生被挑出來的順序,一共有6種可能的組合。
代數運算
社會統計比較常碰到的代數問題在於解決一個未知數,最常運用到移項(transposition)。移項是指將一個數值從方程式等號的一邊移到等號的另外一邊,並改變這個數值的運算符號,以下為移項規則:
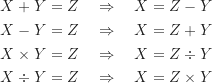
透過上述的移項規則,就可以求得未知數。依照上面移項規則的順序,分別舉一個例子來練習:
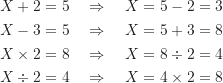
稍微複雜一點的移項可能牽涉到除法運算,例如標準分數和常態曲線下面積之應用裡面的計算。以下舉個未知數![]() 在分子的例子,並示範求得
在分子的例子,並示範求得![]() 的過程。
的過程。
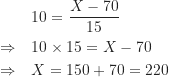
四捨五入
社會統計的數值運算結果若無法整除,須運用捨入(rounding)規則,把數值取到小數點後第2位或第3位。不過,不同於較常使用的四捨五入,社會統計採用一種更精確的捨入規則,稱為四捨六入五成雙,藉此減少分析時的系統偏誤。捨入規則的步驟如下:
- 先確認要保留的小數位數,然後在要保留的小數位數後面置入一個倒v的插入符號。舉例來說,若要把26.32459取到小數點後第2位,將數值標示成26.32^459。
- 把插入符號右邊數字的第1個數字前加入一個小數點,使其變成一個小數,然後比較這個小數和0.5,如果這個小數小於0.5,就直接捨去。在上面的例子裡,把459變成0.459,再和0.5比較,因為0.459小於0.5,所以直接捨去,26.32459變成26.32。
- 如果插入符號右邊的小數大於0.5,則插入符號左邊的數字加1。例如把26.32519取到小數點後第2位,因為0.519大於0.5,所以26.32519進位成26.33。
- 如果插入符號右邊的小數剛好等於0.5,則視插入符號左邊的數字為奇數或偶數來決定捨入。
- 若插入符號左邊的數字為奇數,把數字加1。例如把26.31500取到小數點後第2位,因為0.500剛好等於0.5且1為奇數,所以26.31500進位成26.32。
- 若插入符號左邊的數字為偶數,保留原來的數字。例如把數值26.32500取到小數點後第2位,因為0.500剛好等於0.5且2為偶數,所以26.32500變成26.32。
| 數值 | 插入符號 | 評估部分 | 和 0.5 比較 | 捨入結果 | |
|---|---|---|---|---|---|
| 26.32459 | 26.32^459 | .459 | < 0.5 | 26.32 | |
| 26.32519 | 26.32^519 | .519 | > 0.5 | 26.33 | |
| 和 0.5 比較 | 插入符號左邊數字 | ||||
| 26.31500 | 26.31^500 | .500 | = 0.5 | 奇數 | 26.32 |
| 26.32500 | 26.32^500 | .500 | = 0.5 | 偶數 | 26.32 |
當進行運算的時候,在達到最後的結果前,中間可能會經過許多步驟。在中間的運算步驟,不要做任何的捨入,若是紙筆運算則儘可能保留多一點的小數位數,一直到最後的統計量再進行捨入,以避免過大的進位誤差。
以上為社會統計常用的基本數學符號和運算,雖然都是些簡單的概念和算術運算,但熟習他們將會使社會統計的學習更容易上手。希望透過這些簡單數學的複習,能夠讓不喜歡數學或遠離數學很久的您重拾一些對數學的感覺喔。
若您喜歡本篇文章,請將本網站加入書籤,作為您的學習工具,並持續回訪本網站喔!此外,也歡迎您追蹤本網頁的 Facebook 和/或 X(Twitter)專頁喲!
如果您覺得本篇文章對您有幫助,歡迎買杯珍奶給 Dr. Fish!小小珍奶,大大鼓勵,您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔!