如何使用 Excel 計算離群值排除後的平均數和標準差

離群值（outlier）是一個非常不同於其他資料的數值，在社會統計分析裡，可能會造成偏誤的分析結果，使研究人員做出不正確的研究結論。因此，在資料整理的階段，先瞭解資料的全貌並探索是否有離群值的存在，會是一個重要的過程且有助於之後分析結果的解釋。

在〈離群值對社會統計分析的影響和察覺方法〉裡提到了離群值可以透過圖形或原始分數轉換成標準分數的方式來察覺，當發現了潛在的離群值後，即可利用離群值排除前和排除後的資料來進行分析，並比較兩種結果的差異。最容易受到離群值影響的描述統計量為平均數和標準差，而這兩個數值都可透過 Excel 函數簡單地取得，若資料存在離群值，也有相關的函數可以適用，下面介紹如何在工作表裡計算離群值排除後的平均數和標準差。

• 離群值排除後的平均數
  • AVERAGEIF 函數
  • AVERAGEIFS 函數
  • TRIMMEAN 函數
• 離群值排除後的標準差

離群值排除後的平均數

當利用圖形或原始分數轉換成標準分數的方式而發覺潛在的離群值後，為了瞭解離群值對集中趨勢的影響，可以嘗試計算離群值排除後的平均數，看看和離群值排除前的平均數有何不同。此時在微軟的工作表裡，能夠利用 AVERAGEIF 或 AVERAGEIFS 函數來計算離群值排除後的平均數。

如果要排除的離群值落在一特定數值之下或一特定數值之上，也就是篩選標準只有一個的時候，可以使用 AVERAGEIF 函數。然而，如果要排除的離群值落在一特定數值之下和一特定數值之上，也就是篩選標準有兩個的時候，則可使用 AVERAGEIFS 函數。

❶ AVERAGEIF 函數

先來看只有一個離群值的情況，假設有30位學生的社會統計小考成績，透過散布圖、直方圖或盒形圖發現有一位學生的成績為32分，遠低於其他學生的成績，因此這成績被視為潛在的離群值。若包含這個離群值，成績位於儲存格B2到B31，利用語法 =AVERAGE(B2:B31) 可以計算出平均成績為68.7。

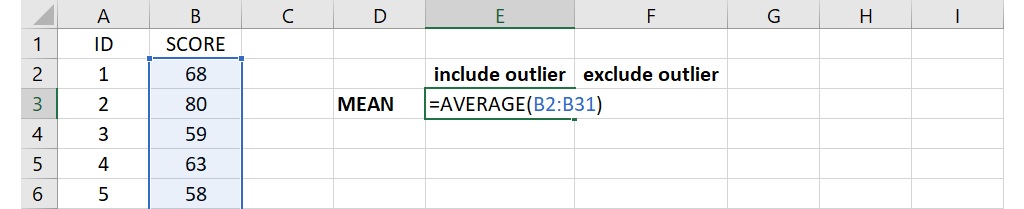
若要排除離群值，也就是不包含成績32分，可以利用 AVERAGEIF 函數來計算平均數。在工作表的儲存格（下圖為儲存格F3）裡輸入下面的語法：

=AVERAGEIF(B2:B31, “> 32”)

語法裡的第1個引數為成績所在的儲存格範圍，第2個引數為成績篩選的標準，建議使用雙引號包住篩選條件，整個語法要求計算大於32分的學生成績之平均數。

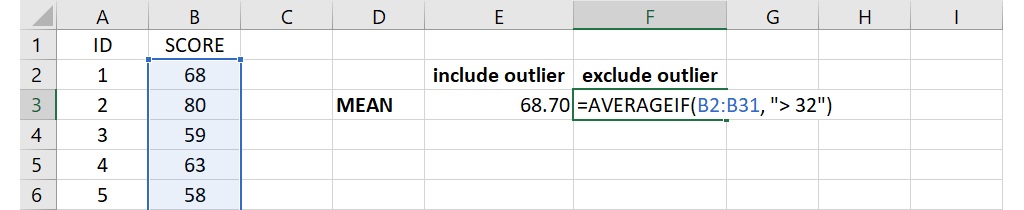
語法輸入完成後按下 Enter 會得到69.97，可以看出這個數值高於包含離群值的平均數68.7。若全部資料都沒有符合篩選的標準時，這函數會傳回「#DIV/0!」的錯誤訊息，因此在定義篩選標準時須特別注意。

❷ AVERAGEIFS 函數

進一步來看，若有兩個離群值，一個值太小而另一個值太大，也就是分布於相反的方向，此時就須使用兩個篩選標準。假設有30位學生的心理學期末考成績，透過圖形檢視，發現有兩位學生的成績特別偏離其他學生的成績，分別為最低分的30分和最高分的98分，可被視為潛在的離群值。

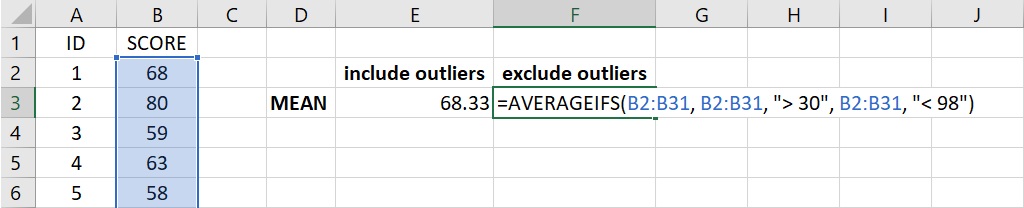
這30位學生的成績位於工作表的儲存格B2到B31，利用 AVERAGE 函數計算得到離群值排除前的成績平均數為68.33。若要排除兩個離群值來計算成績平均數，可以使用 AVERAGEIFS 函數來定義兩個篩選條件，在工作表的儲存格（下圖為儲存格F3）裡輸入下面的語法：

=AVERAGEIFS(B2:B31, B2:B31, “> 30”, B2:B31, “< 98”)

語法裡的第1個引數為成績所在的儲存格範圍，第2和第3個引數分別為第1個篩選條件的資料所在的儲存格範圍和篩選的標準，第4和第5個引數分別為第2個篩選條件的資料所在的儲存格範圍和篩選標準。整個語法要求計算大於30分且小於98分的成績平均數，語法輸入完成後按下 Enter 會傳回68.64，比離群值排除前的平均數高了一點點。

當使用 AVERAGEIFS 函數時，須定義至少一個篩選標準，至多可以定義127個篩選標準。此外，篩選條件的資料範圍須和第1個引數的資料範圍相同，工作表才能傳回計算結果。

❸ TRIMMEAN 函數

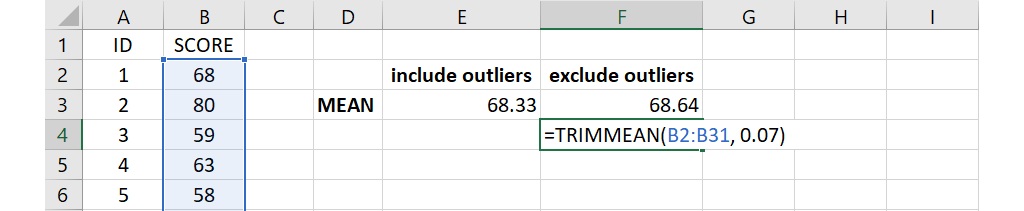
在離群值有兩個且位於相反方向的情況下，除了 AVERAGEIFS 函數之外，還可以使用 TRIMMEAN 函數。在儲存格裡輸入下面的語法：

=TRIMMEAN(B2:B31, 0.07)

語法裡的第1個引數為成績所在的儲存格範圍，第2個引數為被排除分數占所有分數的比例。因為這裡要排除兩個離群值，占所有分數的0.07，所以第2個引數為0.07。整個語法要求排除最大值和最小值並計算出平均數，語法輸入完成後按下 Enter 會傳回68.64，和 AVERAGEIFS 函數傳回的結果是一樣的。

雖然利用 TRIMMEAN 函數能夠很簡單地計算離群值排除後的平均數，但是這函數只能適用在資料兩端都有離群值且離群值數目相同的情況，若離群值只位在資料的一端或資料兩端的離群值數目不一樣時就無法使用。舉例來說，若數值過小的離群值有兩個而數值過大的離群值只有一個，由於要排除的資料數並不對稱，所以無法使用 TRIMMEAN 函數。因此，相較之下，AVERAGEIFS 函數在使用上具有較大的彈性。

離群值排除後的標準差

除了集中趨勢測量的平均數之外，變異性測量裡的標準差也很容易受到離群值的影響。由於推論統計裡的標準誤是從標準差計算而來，代表著離群值也會影響到信賴區間的計算和假設檢定過程中的各種檢定統計量。

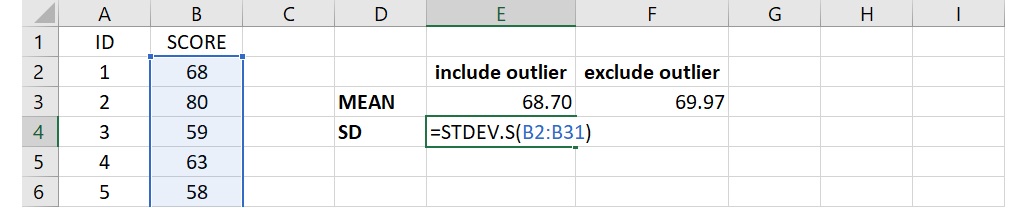
不同於有獨立函數可以使用的平均數計算，工作表裡離群值排除後的標準差計算要透過在標準差函數裡嵌入 IF 函數的方式來達成。同樣以上面30位學生的社會統計小考成績的例子來說，成績位於儲存格B2到B31且有一個32分的離群值，若不排除這個離群值，運用語法 =STDEV.S(B2:B31) 可以得到全部樣本的標準差為11.88。

若要排除32分的離群值，可以在標準差函數裡嵌入 IF 函數。因為要排除32分，也就是只利用大於32分的學生成績來計算標準差，所以可在儲存格（下圖為儲存格F4）裡輸入下面的語法：

=STDEV.S(IF(B2:B31 > 32, B2:B31))

內嵌的 IF 函數裡第1個引數為篩選條件，第2個引數為篩選條件滿足時傳回的數值。利用這樣的語法，當一個成績滿足篩選條件時，會保留原本的成績；當一個成績沒有滿足篩選條件時，儲存格裡的成績會變成 FALSE，而這成績就不會被列入計算。最後，STDEV.S 函數就會使用被篩選出來的成績來計算標準差。

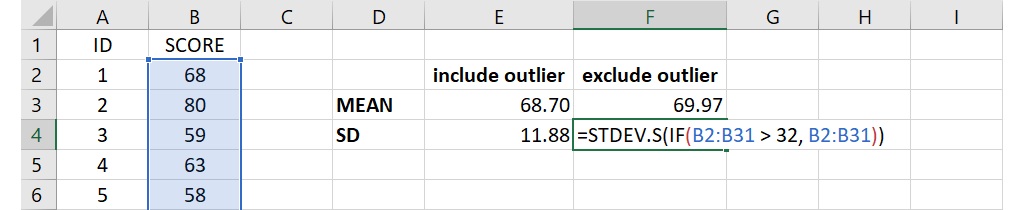
語法輸入完成後，按下 Enter 會傳回9.81，這個數值明顯地小於離群值排除前的標準差。從計算結果可以發現，當離群值排除後，平均數變大而標準差變小了。

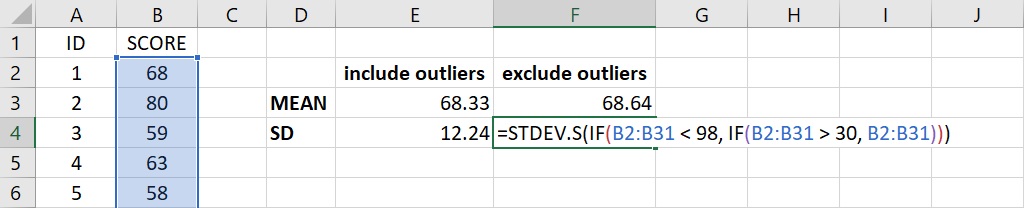
若是有兩個位於資料兩端的離群值，則要在標準差函數裡內嵌兩個 IF 函數。以上面30位學生的心理學期末考成績為例，成績位於儲存格B2到B31，兩個潛在的離群值分別為最低分的30分和最高分的98分。若不排除兩個離群值，全部樣本的標準差為12.24。如果要排除這兩個離群值再計算樣本標準差，可以在儲存格（下圖為儲存格F4）裡輸入下面的語法：

=STDEV.S(IF(B2:B31 < 98, IF(B2:B31 > 30, B2:B31)))

這個語法使用了兩個 IF 函數，第2個 IF 函數篩選出大於30分的成績，第1個 IF 函數再從大於30分的成績裡篩選出小於98分的成績，最後 STDEV.S 函數再計算被篩選出來的大於30分且小於98分成績的標準差。語法輸入完成後，按下 Enter 會傳回8.59，可以看到這個數值明顯地小於離群值排除前的標準差。

標準差函數裡內嵌 IF 函數的語法具有很大的彈性，不論離群值只位於資料的一端或位於資料的兩端，都可以運用這樣的語法來排除離群值再計算標準差。從計算結果可以看到，在兩個離群值的例子裡，離群值排除後，平均數稍微變大而標準差明顯地變小了。

簡單來說，在工作表裡可以很簡單地運用函數來計算離群值排除後的平均數和標準差。雖然您也可以先在工作表裡刪除離群值的資料再利用 AVERAGE 和 STDEV.S 函數來計算平均數和標準差，但這樣的方式會變更原始資料，資料分析的過程中較不建議這樣的做法。在保留原始資料的情況下，利用函數排除離群值再計算平均數和標準差會是個較合適的方法喔！

以上為本篇文章對如何使用 Excel 計算離群值排除後的平均數和標準差之介紹，希望透過本篇文章，您學會了利用各種不同的函數排除離群值後再計算平均數和標準差的方法。若您喜歡本篇文章，請將本網站加入書籤，並隨時回訪本網站喔！另外，也歡迎您追蹤本網站的 Facebook 和／或 X（Twitter）專頁喲！

如果您覺得本篇文章對您有幫助，歡迎買杯珍奶給 Dr. Fish！小小珍奶，大大鼓勵，您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔！