行為和社會科學研究很常使用卡方獨立性檢定去探討類別變項之間的關係，當顯著性檢定的結果指出變項之間存在關聯性時，並沒有同時顯示這層關聯的程度，也就是效果量的大小。若要瞭解效果量，需要進一步的分析，而很多時候我們會用關聯性測量來呈現效果量，例如 phi、列聯係數和 Carmér′s V，這方面的說明可以參考卡方獨立性檢定的效果量：關聯性測量。
雖然關聯性測量是呈現類別變項效果量的一種很好的方法，而且介於0和1的數值也容易理解，但這些數值除了指出變項間為低、中、高的關聯程度外，並無法再做任何有意義的解釋。另一種可以用來呈現類別變項效果量的方法為勝率比（odds ratio），雖然比較適合用在2X2列聯表上，但解釋和實用性上都比關聯性測量略勝一籌。
本篇文章將介紹勝率比呈現卡方獨立性檢定效果量的方法，並舉例說明，再示範運用 SPSS 取得勝率比的操作方法。由於卡方獨立性檢定為本篇文章的基礎，如果您不清楚或不熟悉這種統計檢定，建議您先閱讀卡方獨立性檢定的假設檢定，將有助於下面內容的理解喔！
勝率比的概念
勝率比可用來測量不同的研究情境（或實驗情境）和發生結果之間的關聯，英文為 odds ratio，有些中文翻譯為勝算比。換句話說，勝率比是不同的研究情境所產生結果之間的比較。
勝率比來自於2個勝率（odds）的比較，因此在說明勝率比之前須先瞭解勝率的意義。勝率也可說是機率、可能性，指一個事件發生的機率除以一個事件沒有發生的機率，在類別變項組成的列聯表裡，指一個類別裡一個事件發生的次數除以一個事件沒有發生的次數。
當有2個類別或情境時，會有2個勝率，而這2個勝率的比較就是勝率比，能夠呈現出2個類別或情境的關聯強度。也就是說，勝率比可以指出，相較於一個類別或情境的結果，另一個類別或情境結果的發生可能性有多大。
上面勝率比的公式裡，分母通常是對照類別或控制組的勝率，藉此勝率比才可以指出分子的類別或情境比較容易或不容易發生。例如實驗組和控制組的研究設計，勝率比可告訴我們實驗組結果的發生可能性較控制組結果的發生可能性來得高或低。
勝率比通常會以1作為分界點，因為當勝率比為1時，分子和分母的勝率是相同的，代表不同的類別或情境和結果的發生之間沒有關聯。勝率比小於1時，分子的勝率小於分母的勝率，代表分子的類別或情境發生的可能性較小；勝率比大於1時，分子的勝率大於分母的勝率，代表分子的類別或情境發生的可能性較大。
當用勝率比來呈現卡方獨立性檢定的效果量時，較適合用在2X2列聯表上，此種情況下最能透過勝率比做出有意義的解釋。若是較大的列聯表，也就是超過2個類別或情境時，勝率也會超過2個，此時勝率比要以何種方式呈現，在解釋上就會有困難。除非類別或情境是具有次序的變項（測量尺度為次序尺度），可將一個類別作為基準或對照類別，再計算出其他類別或情境和這個基準或對照類別的勝率比，解釋上就會變得較有意義。
勝率比的例子
假設有位研究人員想探討居住地區和對陌生人幫助行為之間的關係，她給250位研究參與者一個陌生人需要幫助的假想情境，並調查他們的幫助意願。若居住地區的2個類別為鄉村和城市，而幫助行為的2個類別為幫助和不幫助，居住地區和幫助行為構成的列聯表如下。如果顯著水準（α水準）為0.05，使用卡方獨立性檢定，試問：
- 顯著性檢定的結果為何？
- 若居住地區和陌生人幫助行為之間有關聯，試用勝率比說明兩者間的效果量。
| 鄉村 | 城市 | 列合計 | |
|---|---|---|---|
| 幫助 | 75 | 50 | 125 |
| 不幫助 | 45 | 80 | 125 |
| 欄合計 | 120 | 130 | 250 |
這個研究想探討對陌生人的幫助行為是否會因為居住地區的不同而有差異，研究假設的虛無假設和對立假設分別如下：
- 虛無假設（
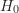）：居住地區和對陌生人的幫助行為彼此獨立。 - 對立假設（
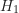）：居住地區和對陌生人的幫助行為具有關聯。
由於居住地區和對陌生人的幫助行為皆為二分變項，所以使用卡方獨立性檢定來檢視2個變項之間的關係。為了求得卡方檢定統計量，須先計算列聯表裡各個細格的期望次數，例如「住在鄉村且願意幫助」細格的期望次數為：
![\[ \frac {125 \times 120}{250} = 60 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-36c4b252243fdfbb6328b49a316a32d6_l3.png "Rendered by QuickLaTeX.com")
透過相同的計算方法，求得各個細格的期望次數，完成後各個細格的觀察次數和期望次數（每個細格括號裡的數值）如下表。若您不清楚卡方檢定統計量的公式和計算方法，請參考卡方獨立性檢定的假設檢定。
| 鄉村 | 城市 | 列合計 | |
|---|---|---|---|
| 幫助 | 75 (60) |
50 (65) |
125 |
| 不幫助 | 45 (60) |
80 (65) |
125 |
| 欄合計 | 120 | 130 | 250 |
接著，利用上表中各個細格裡的觀察次數和期望次數來計算卡方檢定統計量，把計算過程中無法整除的數值四捨五入到小數點後第5位而最後的數值四捨五入到小數點後第3位，過程如下：
![\begin{align*}\chi^2 &= \frac {(75-60)^2}{60} + \frac {(50-65)^2}{65} + \frac {(45-60)^2}{60} + \frac {(80-65)^2}{65} \\[5pt]&= 3.75 + 3.46154 + 3.75 + 3.46154 \\[5pt]&= 14.423\end{align*}](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-6cb7c38d710bc267f104727cabb4a5c1_l3.png "Rendered by QuickLaTeX.com")
因為這裡為2X2列聯表，所以自由度為
。查詢卡方分配臨界值表，在α水準為0.05且自由度為1的時候，卡方臨界值為3.841。
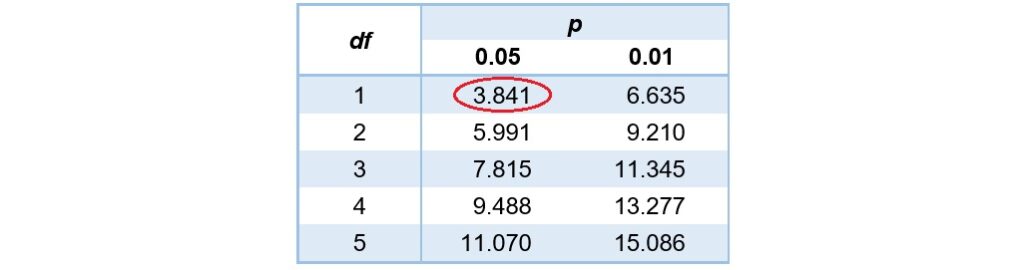
最後，運用決策規則，比較卡方檢定統計量和臨界值，因為
，所以拒絕虛無假設，接受對立假設。卡方獨立性檢定的分析結果指出，居住地區和對陌生人的幫助行為有關聯。
由於分析結果指出居住地區和對陌生人的幫助行為有關聯，所以可進一步探索效果量。這裡使用勝率比來呈現效果量，先分別探討鄉村和城市對陌生人幫助行為的勝率。
➀ 居住在鄉村且願意幫助陌生人的勝率
![\[ \text {odds}_{\text {rural}} = \frac {\text {help}}{\text {not help}} = \frac {75}{45} \approx 1.667 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-bbb17cd7332742e2ab0f96a0240bab7e_l3.png "Rendered by QuickLaTeX.com")
➁ 居住在城市且願意幫助陌生人的勝率
![\[ \text {odds}_{\text {urban}} = \frac {\text {help}}{\text {not help}} = \frac {50}{80} = 0.625 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-da11c896252bd628dc47bce82cd39b28_l3.png "Rendered by QuickLaTeX.com")
利用上面的2個勝率，就可簡單地計算出勝率比。把居住在鄉村且願意幫助陌生人的勝率放在分子，而居住在城市且願意幫助陌生人的勝率放在分母，勝率比為：
![\[ \text {odds ratio} = \frac {\text {odds}_{\text {rural}}}{\text {odds}_{\text {urban}}} = \frac {1.667}{0.625} =2.6672 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-78e3741dd04b9c2e35394c6655eb7285_l3.png "Rendered by QuickLaTeX.com")
計算結果顯示勝率比為2.6672，這個數值指出居住在鄉村且願意幫助陌生人的可能性為居住在都市且願意幫助陌生人的2.6672倍。
不像關聯性測量呈現的效果量，只能用一個數值來表示2個類別變項之間的關聯程度，透過勝率比，可以更細緻地探討變項裡各個類別的關係，並且能夠用更有意義的數值來做解釋。因此，若要呈現卡方獨立性檢定的效果量，且2個變項皆為二分變項時，勝率比會是個比關聯性測量更好的方法。
運用 SPSS 取得勝率比
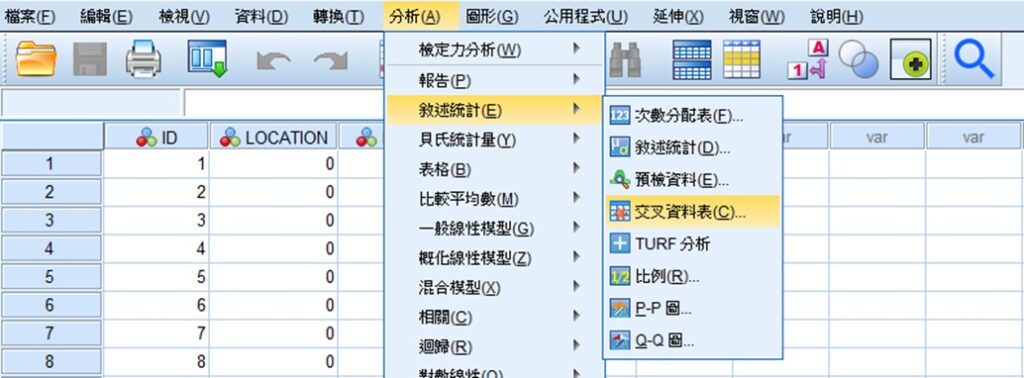
這裡使用上面例子的原始資料來示範 SPSS 的操作方法，您也可以使用自己的資料來練習。在 SPSS 資料編輯器視窗，點選功能表的分析 » 敘述統計» 交叉資料表，帶出「交叉表」視窗。關於 SPSS 的操作介面和資料輸入方法，請參考 SPSS操作環境和資料輸入。
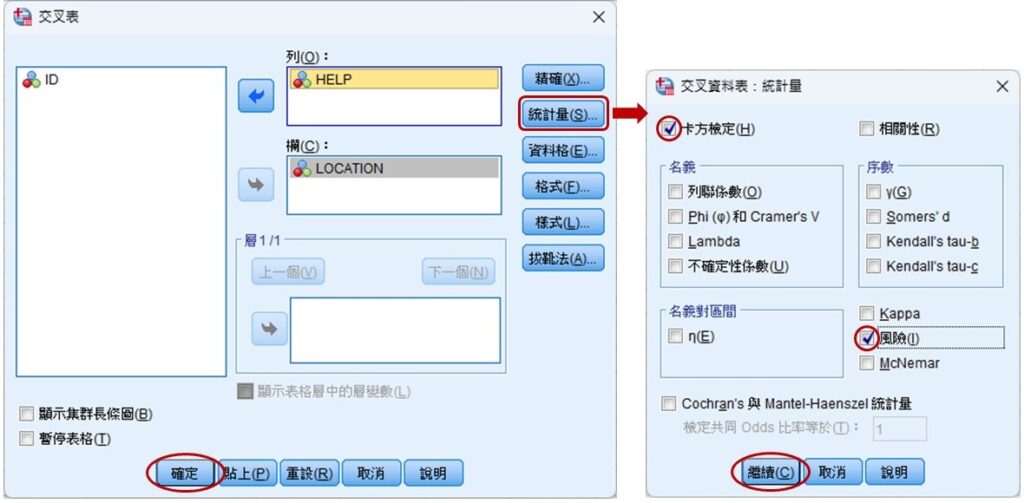
在「交叉表」視窗裡，把一個變項移至列(O)，另一個變項移至欄(C)，然後點選視窗右側的統計量(S)。在「交叉資料表：統計量」視窗裡，勾選卡方檢定(H)和風險(I)，完成後按下視窗下方的繼續(C)。回到「交叉表」視窗後，再按下確定。
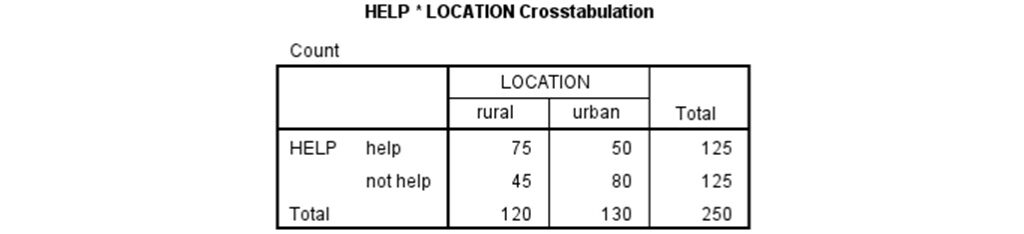
經過上述的步驟，SPSS 會輸出一個2個類別變項的列聯表，這個列聯表裡各個細格的數值和上面例子的列聯表是一樣的。
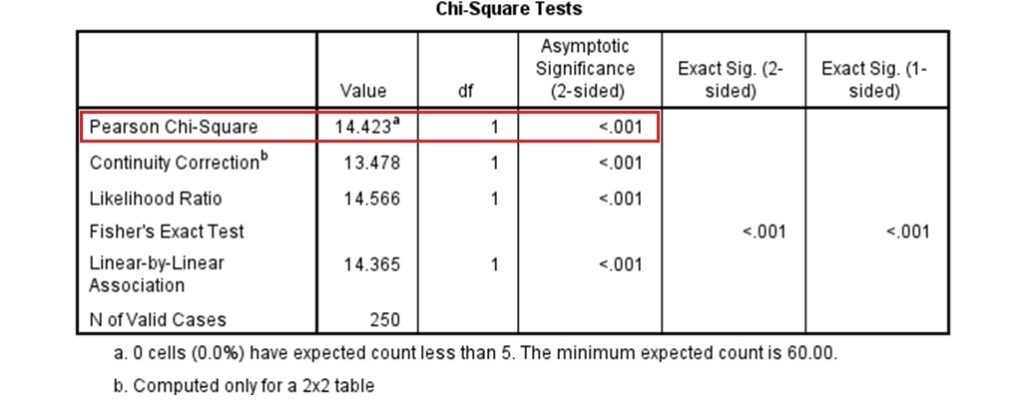
列聯表的下方是如下的卡方檢定結果表，從表中可以看出，卡方檢定的檢定統計量（Pearson Chi-Square）為14.423，自由度為1，而獲得這個檢定統計量的機率（
值）小於0.001。因為值小於α水準0.05，所以可拒絕虛無假設，分析結果指出居住地區和對陌生人的幫助行為有關聯。
您也可以參考概似比檢定的結果，就是下表中 Likelihood Ratio 那一列的數值。概似比檢定運用最大概似理論來分析列聯表，同樣使用卡方檢定統計量，當樣本數很大時，概似比檢定和卡方檢定的結果會差不多。關於更深入的概似比檢定的介紹，可以參考概似比檢定：類別資料分析的另一種選擇。
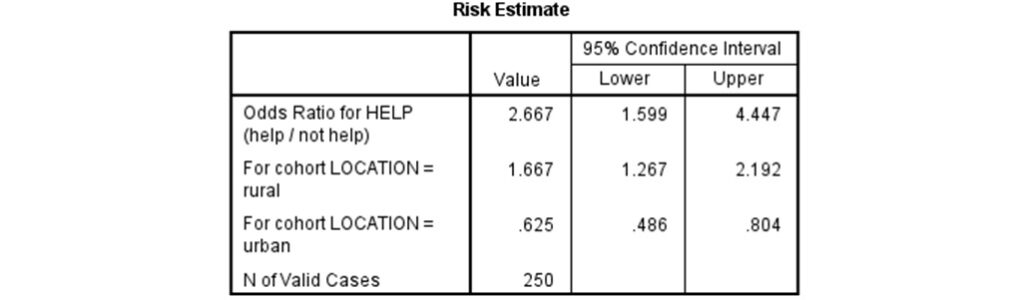
由於假設檢定結果指出2變項有關聯，所以可進一步看檢定結果表下方的勝率比表格。從下表可以看到，當居住地區為鄉村（rural）時，幫助陌生人的勝率為1.667；當居住地區為城市（urban）時，幫助陌生人的勝率為0.625。勝率比即為住在鄉村幫助陌生人的勝率除以住在城市幫助陌生人的勝率，就是下表 Odds Ratio for HELP 的數值2.667，這些結果都和上面紙筆計算的結果相同。
之前探討過的關聯性測量和這裡介紹的勝率比同樣都是呈現卡方獨立性檢定效果量的方法，關聯性測量用一個類似相關係數的數值來說明2個類別變項之間的關聯強度，而勝率比用更具意義的方法來說明變項裡一個類別和另一個類別的關係，是一種更細緻也更容易理解的呈現方法。依據研究的目的和研究假設，您可以選擇合適的效果量呈現方法。
以上為本篇文章對卡方獨立性檢定效果量的介紹，希望透過本篇文章，您瞭解了勝率和勝率比的意義和計算方法，也學會了運用 SPSS 取得勝率比的操作過程。若您喜歡本篇文章，請將本網站加入書籤，並隨時回訪本網站喔！另外，也歡迎您追蹤本網站的 Facebook 和／或 X（Twitter）專頁喲！
如果您覺得本篇文章對您有幫助，歡迎買杯珍奶給 Dr. Fish！小小珍奶，大大鼓勵，您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔！
