社會統計基礎的機率認識【運算規則篇】

社會統計基礎的機率認識【定義和專有名詞篇】介紹了古典和經驗觀點的機率定義，也列出了幾個常見的機率專有名詞。在專有名詞裡，簡單地提到了獨立事件和互斥事件的機率運算方法，希望能讓學習者有基本的認識。

本篇文章將更完整地介紹社會統計基礎的機率運算規則，也就是加法規則和乘法規則。數學領域的機率運算可能相當的複雜和困難，甚至能夠開設一門專門課程。幸好基礎的社會統計機率運算僅有加法規則和乘法規則，雖然不像吃糖果般地「甜」，但也不至於像喝苦茶般地「苦」，是理解推論統計檢定結果的一個重要基礎。下面內容將先介紹加法規則再介紹乘法規則，並舉例子說明各個規則的計算方法。

加法規則
乘法規則
加法規則和乘法規則合併使用
機率運算在列聯表的應用

加法規則

當想要決定數個可能事件裡任何一個事件的發生機率，就須使用加法規則（addition rule）。例如，從親密伴侶受虐者裡抽取到一位身體虐待或精神虐待的受虐者機率，或從受刑人裡抽取到一位憂鬱症患者或藥物成癮者的機率。

為了讓說明簡單化，假設只有A和B兩種可能的事件，在這樣的情況下，事件A或事件B的發生機率為事件A的發生機率加事件B的發生機率減事件A和事件B共同發生的機率。若讓 $p(A)$ 代表事件A的發生機率， $p(B)$ 代表事件B的發生機率， $p(A \ \text{and} \ B)$ 代表事件A和B共同發生的機率，加法規則的公式如下：

(1) $\begin{equation*}p(A \ \text{or} \ B) = p(A) + p(B) - p(A \ \text{and} \ B)\end{equation*}$

舉例來看，一副撲克牌有黑桃、梅花、紅心和方塊4種花色，黑桃和梅花為黑色而紅心和方塊為紅色，每種花色各有13張牌，分別為A、數字2到10、J、Q和K。若從一副撲克牌裡隨機抽取出1張牌，試問這張牌為人頭牌（也就是J、Q或K）或黑桃的機率是多少？

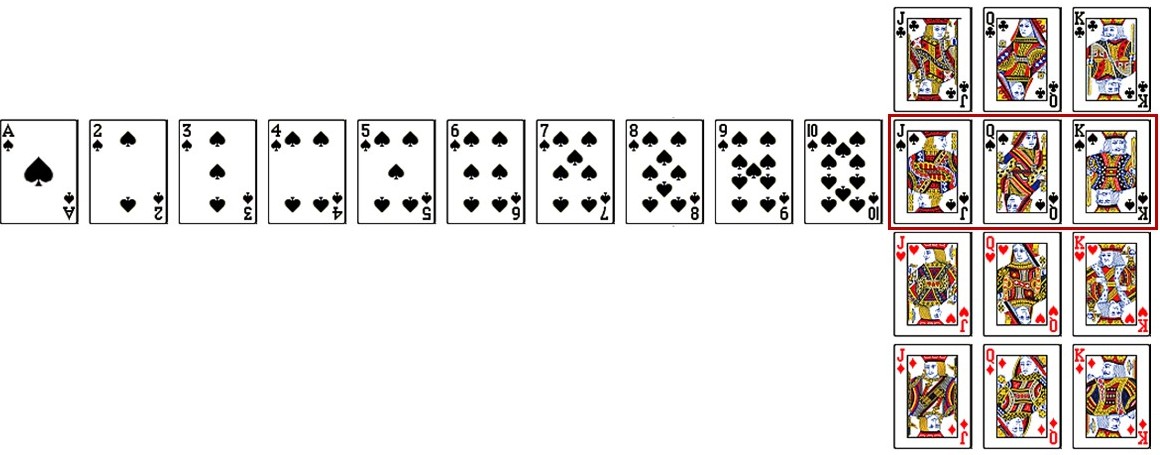
為了方便機率計算，可先把需要的資訊列出來，再利用上面的公式(1)來計算。一副撲克牌共有52張牌，請參考上圖，人頭牌J、Q和K共12張，黑桃共13張，同有人頭和黑桃的牌共3張（上圖紅框裡的牌），因此隨機抽取1張牌，把計算結果四捨五入到小數點後第4位，這張牌為人頭牌或黑桃的機率為：

$\begin{equation*}\begin{CJK*}{UTF8}{bsmi}\begin{align*}p(\text{人頭或黑桃}) &= p(\text{人頭})+p(\text{黑桃})-p(\text{人頭和黑桃}) \\[5pt]&= \frac {12}{52} + \frac {13}{52} - \frac {3}{52} \\[5pt]&\approx 0.4231\end{align*}\end{CJK*}\end{equation*}$

上面的例子裡，因為事件A和事件B會同時發生，所以機率計算時須減去2事件同時發生的機率才是事件A或事件B發生的機率。不過當2個事件為互斥事件（mutually exclusive events），也就是2個事件不可能同時發生時，公式(1)的 $p(A \ \text{and} \ B) = 0$ ，加法規則可以簡化成下面的公式：

(2) $\begin{equation*}p(A \ \text{or} \ B) = p(A) + p(B)\end{equation*}$

同樣以撲克牌為例，沒有任何1張牌既是黑桃又是紅心，所以黑桃和紅心就是互斥事件。此外，沒有任何1張牌既是A又是5，所以A和5也是互斥事件。因此，若從一副撲克牌裡隨機抽取出1張牌，試問這張牌為黑桃或紅心的機率是多少？

從上圖可以看出，黑桃的牌有13張，紅心的牌也是13張，由於沒有任何1張牌既是黑桃又是紅心，所以可以利用上面的公式(2)來計算機率。

$\begin{equation*}\begin{CJK*}{UTF8}{bsmi}\begin{align*}p(\text{黑桃或紅心}) &= p(\text{黑桃})+p(\text{紅心}) \\[5pt]&= \frac {13}{52} + \frac {13}{52} \\[5pt]&= 0.5000\end{align*}\end{CJK*}\end{equation*}$

從計算結果可以發現從一副撲克牌裡隨機抽取出1張牌，這張牌為黑桃或紅心的機率為0.5000。若從常理來看，黑桃和紅心的牌剛好占了一副撲克牌的一半，這樣的結果也就不難理解了。

再舉一個例子，1顆骰子有6個面，每一面都有不同數目的小圓點，從1個點到6個點，不會重複出現，所以骰子的面與面之間為互斥事件。如果擲1顆骰子一次，試問得到1個點或4個點的機率是多少？

從上圖可以看到，只有一面為1個點，也只有一面為4個點，而且沒有任何一面既有1個點也有4個點（代表1個點和4個點不會同時出現），所以可以利用上面的公式(2)來計算機率。

$\begin{align*}p(\text{1 or 4}) &= p(1) + p(4) \\[5pt]&= \frac {1}{6} + \frac {1}{6} \\[5pt]&\approx 0.3333\end{align*}$

計算結果指出擲1顆骰子一次，得到1個點或4個點的機率為0.3333。因此，當事件之間互斥時，加法規則的運算變得簡單許多。

乘法規則

當想要決定數個事件同時發生或連續發生的機率時，須使用乘法規則（multiplication rule）。例如，尋求心理諮商的個案為生理女性且受到親密伴侶精神虐待的機率，或受刑人裡為藥物濫用者且具有大學學歷的機率。

乘法規則和加法規則最大的差別在於乘法規則適用在數個事件一起發生的情況，而加法規則適用在一個事件發生的情況。為了簡化說明，假設只有A和B兩個事件，讓 $p(A \ \text {and} \ B)$ 表示2個事件一同發生的機率，稱為聯合機率，乘法規則可分成下面的3種情況來討論。

❶ 兩個事件為互斥事件

若2個事件為互斥事件，代表一個事件的發生排除了另一個事件的發生，也就是說這2個事件不會同時發生，所以 $p(A \ \text {and} \ B) = 0$ 。

❷ 兩個事件為獨立事件

若2個事件為獨立事件（independent events），代表一個事件的發生不會影響另一個事件的發生。兩個獨立事件的同時發生機率為A事件發生機率和B事件發生機率的乘積，公式如下：

(3) $\begin{equation*}p(A \ \text {and} \ B) = p(A) \times p(B)\end{equation*}$

放回抽樣（sampling with replacement）可用來說明獨立事件的乘法規則。舉例來說，一個箱子裡有3種顏色的球：2顆綠色球、3顆紅色球和5顆藍色球，若要抽出2顆球，一次抽出1顆球，第1次抽出球之後把抽出的球放回箱子裡再進行第2次的抽取，使得第2次抽球時箱子裡仍維持原本的10顆球。因為第2次還是可能抽到第1次抽出來的球，所以這2次的抽球為獨立事件。

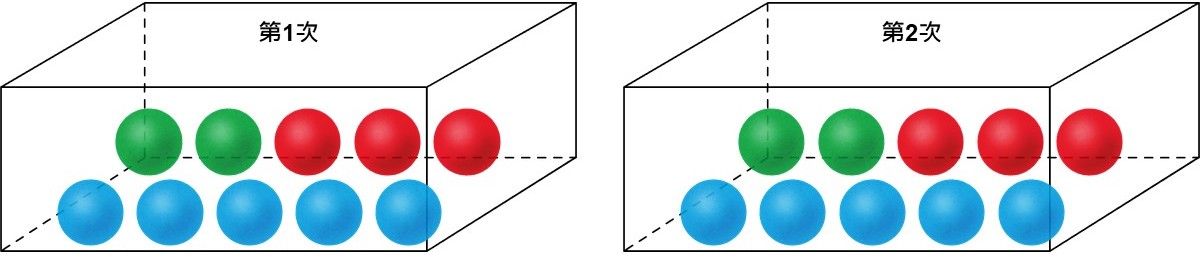
illustration of sampling with replacement

在這個例子裡，如果要抽出2顆球，一次抽1顆球，第1次抽出後再放回，試問2顆球都是紅色的機率為多少？因為箱子裡共有10顆球，紅色的球有3顆，再加上2次的抽取為獨立事件，所以若事件A為第1次抽到紅球的機率，事件B為第2次抽到紅球的機率，利用上面的公式(3)，2顆球都是紅色的機率為：

$\begin{align*}p(A \ \text {and} \ B) &= \frac {3}{10} \times \frac {3}{10} \\[5pt]&= 0.0900\end{align*}$

計算結果顯示，2顆球都是紅色的機率為0.0900。再舉一個例子，若從一副撲克牌裡抽出2張牌，一次抽出1張牌，第1次抽出後將牌放回再抽第2次，試問2張牌都是5的機率為多少？

illustration of sampling with replacement using cards

這例子和上面抽球的例子一樣，都是放回抽樣，不論是第1次或第2次抽牌，撲克牌都是52張，5的牌都是4張。由於第2次抽牌還是有可能抽到第1次抽出來的牌，也就是第1次抽牌的結果不會影響到第2次抽牌的結果，所以2次的抽牌為獨立事件。若讓事件A為第1次抽到5的機率，事件B為第2次抽到5的機率，2張牌都是5的機率為：

$\begin{align*}p(A \ \text {and} \ B) &= \frac {4}{52} \times \frac {4}{52} \\[5pt]&\approx 0.0059\end{align*}$

因此，從一副撲克牌裡抽2張牌，一次抽出1張，抽出後放回，2張牌都是5的機率為0.0059。從這2個例子可以看到，當2個事件為獨立事件時，事件同時發生的機率為各個事件發生機率的乘積。

❸ 兩個事件為相依事件

若2個事件為相依事件（dependent events），代表一事件的發生會影響另一事件的發生，此時2事件同時發生的機率不再是各個事件發生機率的乘積，而須考量A事件已發生的情況下B事件發生的機率，可用 $p(B \mid A)$ 來表示，稱為條件機率。因此，當2個事件為相依事件時，乘法規則為：

(4) $\begin{equation*}p(A \ \text {and} \ B) = p(A) \times p(B \mid A)\end{equation*}$

不同於上面獨立事件的放回抽樣，相依事件可用不放回抽樣（sampling without replacement）來說明乘法規則。舉例來說，一個箱子裡有3種顏色的球：2顆綠色球、3顆紅色球和5顆藍色球，若要抽出2顆球，一次抽出1顆球，第1次抽出球之後不把抽出的球放回箱子裡就進行第2次的抽取，因此第2次抽球時箱子裡只剩9顆球。由於第2次不可能再抽到第1次抽出來的球，所以這2次的抽球為相依事件。

在這個例子裡，如果要抽出2顆球，一次抽1顆球，第1次抽出後不放回，試問第1次抽到綠球而第2次抽到藍球的機率為多少？

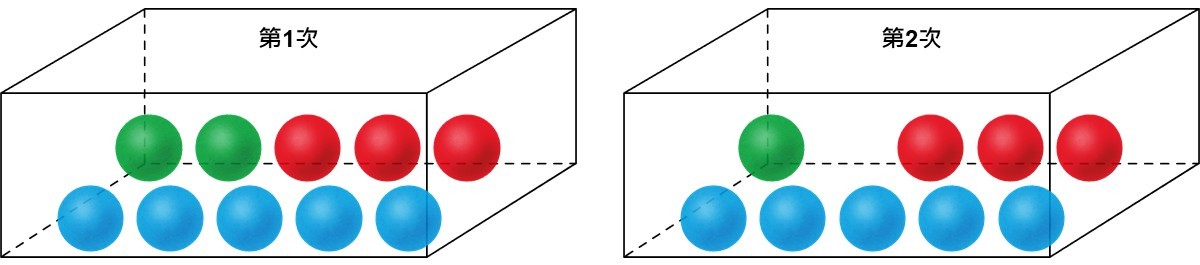
illustration of sampling without replacement

因為箱子裡共有10顆球，綠色球有2顆，所以第1次抽球時抽到綠色球的機率為 $2/10$ 。由於抽出球後不放回，所以第2次抽球時箱子裡剩9顆球，藍色球有5顆，此時抽到藍色球的機率為 $5/9$ 。若讓事件A為第1次抽到綠球的機率，事件B為第2次抽到藍球的機率，抽出後不放回，則依序抽到綠球、藍球的機率為：

$\begin{align*}p(A \ \text {and} \ B) &= p(A) \times p(B \mid A) \\[5pt]&= \frac {2}{10} \times \frac {5}{9} \\[5pt]&\approx 0.1111\end{align*}$

計算結果顯示在抽球後不放回的情況下，依序抽到綠球和藍球的機率為0.1111。再舉上面獨立事件的撲克牌例子，若從一副撲克牌裡抽出2張牌，一次抽出1張牌，第1次抽出後不將牌放回就抽第2次，試問2張牌都是5的機率為多少？

illustration of sampling without replacement using cards

因為撲克牌共有52張，其中5的牌有4張，所以第1次抽牌時抽到5的機率為 $4/52$ 。由於抽出牌後不再放回去，所以第2次抽牌時總牌數變成51張。此外，第1次已經抽出1張5的牌，使得5的牌剩3張，因此第2次抽到5的機率為 $3/51$ 。若讓事件A為第1次抽到5的機率，事件B為第2次抽到5的機率，抽出後不放回，則2次都抽到5的機率為：

$\begin{align*}p(A \ \text {and} \ B) &= p(A) \times p(B \mid A) \\[5pt]&= \frac {4}{52} \times \frac {3}{51} \\[5pt]&\approx 0.0045\end{align*}$

因此，在抽出後不放回的情況下，2次都抽到5的機率為0.0045。從上面的2個例子可以看出，若2事件為相依事件，探討2事件同時發生的機率須考慮到一事件已發生時另一事件發生的機率，與2事件為獨立事件的情況有明顯的不同。

加法規則和乘法規則合併使用

加法規則和乘法規則除了各別使用外，有時候2種規則也會一起使用。舉例來說，上面提到的3種顏色的球：2顆綠色球、3顆紅色球和5顆藍色球，若要抽出2顆球，一次抽出1顆球且抽出後放回，試問若不考量抽出的順序，抽出1顆紅球和1顆藍球的機率是多少？

這個例子會有2種可能的結果：①第1次抽到紅色球而第2次抽到藍色球，②第1次抽到藍色球而第2次抽到紅色球。

illustration of addition rule and multiplication rule

因為抽出後放回，所以第1次和第2次的抽球為獨立事件，可利用上面的公式(3)來分別計算得到第1種結果和第2種結果的機率。讓R代表紅色球而B代表藍色球，第1次抽到紅球而第2次抽到藍球以及第1次抽到藍球而第2次抽到紅球的機率分別為：

$\begin{align*}p(R \ \text{and} \ B) &= p(R) \times p(B) = \frac {3}{10} \times \frac {5}{10} = 0.1500 \\[5pt]p(B \ \text{and} \ R) &= p(B) \times p(R) = \frac {5}{10} \times \frac {3}{10} = 0.1500\end{align*}$

計算結果顯示第1次抽到紅球而第2次抽到藍球的機率為0.1500，且第1次抽到藍球而第2次抽到紅球的機率也為0.1500。透過計算知道了獲得第1種結果和第2種結果的機率後，再利用上面的公式(2)計算得到任何一種結果的機率。讓A代表第1種結果（紅球和藍球）而B代表第2種結果（藍球和紅球），得到A或B結果的機率為：

$\begin{align*}p(A \ \text{or} \ B) &= p(A) + p(B) \\[5pt]&= 0.1500 + 0.1500 \\[5pt]&= 0.3000\end{align*}$

因此，從2顆綠色、3顆紅色和5顆藍色的10顆球裡抽出2顆球，一次抽出1顆球且抽出後放回，抽到1顆紅色球和1顆藍色球的機率為0.3000。

機率運算在列聯表的應用

列聯表是社會統計很常使用到的一種表格，可用來檢視2個變項之間的關係，也是卡方獨立性檢定執行前會製作的一個表格。下面的列聯表顯示受訪者的居住地區和他們對陌生人的幫助行為之間的關係，我們可運用機率運算到這個列聯表，計算簡單機率、聯合機率和條件機率。

	鄉村	城市	列合計
幫助	75	50	125
不幫助	45	80	125
欄合計	120	130	250

讓 Help 代表幫助陌生人、No Help 代表沒有幫助陌生人，若隨機抽取出一個人，這個人會幫助陌生人和不會幫助陌生人的簡單機率分別為：

$\begin{align*}p(\text {Help}) &= \frac {125}{250} = 0.5000 \\[5pt]p(\text {No Help}) &= \frac {125}{250} = 0.5000\end{align*}$

計算結果顯示，不論居住地區，幫助陌生人和不幫助陌生人的機率都是0.5000。進一步來看，讓 Rural 代表鄉村、Urban 代表城市，居住在鄉村且幫助陌生人以及居住在城市且幫助陌生人的聯合機率分別為：

$\begin{align*}p(\text {Rural and Help}) &= \frac {75}{250} = 0.3000 \\[5pt]p(\text {Urban and Help}) &= \frac {50}{250} = 0.2000\end{align*}$

計算結果顯示，居住在鄉村且幫助陌生人的機率為0.3000，高於居住在城市且幫助陌生人的機率0.2000。最後來看條件機率，假設居住在鄉村，一個人幫助陌生人的機率為：

$\begin{equation*}p(\text {Help} \mid \text {Rural}) = \frac {75}{120} = 0.6250\end{equation*}$

因此，居住在鄉村的情況下，一個人會幫助陌生人的機率為0.6250。利用這個條件機率也可以計算出住在鄉村且幫助陌生人的聯合機率，透過兩個事件為相依事件的乘法規則，也就是上面的公式(4)，可以得到下面的結果：

$\begin{align*}p(\text {Rural and Help}) &= p(\text {Rural}) \times p(\text {Help} \mid \text {Rural}) \\[5pt]&= \frac {120}{250} \times \frac {75}{120} \\[5pt]&= 0.3000\end{align*}$

利用相依事件的乘法規則計算出來的聯合機率和上面直接利用「居住在鄉村且幫助陌生人」那一細格所計算出來的聯合機率是一樣的，同樣都是0.3000。

這裡有一點要注意的地方，居住在鄉村的情況下一個人幫助陌生人的條件機率並不同於幫助陌生人的情況下一個人居住在鄉村的條件機率。在幫助陌生人的情況下，一個人居住在鄉村的機率為：

$p(\text {Rural} \mid \text {Help}) = \frac {75}{125} = 0.6000$

這結果明顯地不同於居住在鄉村的情況下一個人會幫助陌生人的機率（0.6250），代表列聯表裡條件機率並不是對稱的。至於要使用哪一個條件機率，就取決於您的研究目的和研究問題了。

上面內容提到的例子皆為間斷變項，例如抽1張撲克牌、擲1顆骰子和抽1顆球，但社會或行為科學的研究很常使用連續變項，其機率計算的方法和間斷變項稍有不同，若有興趣瞭解更多，可以參考連續變項的機率計算。

以上為本篇文章對社會統計基礎的機率運算規則的介紹，希望透過本篇文章，您瞭解了基礎的機率運算規則，也學會了運算的方法。若您喜歡本篇文章，請將本網站加入書籤，並隨時回訪本網站喔！另外，也歡迎您追蹤本網站的 Facebook 和／或 X（Twitter）專頁喲！

如果您覺得本篇文章對您有幫助，歡迎買杯珍奶給 Dr. Fish！小小珍奶，大大鼓勵，您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔！