比率、比例和百分比的差別

當閱讀報章雜誌時，很常看到「幼兒園師生比」、「房貸占收入的比例」、「業績成長百分比」等文字。此外，撰寫研究報告時也很常使用比率、比例或百分比來描述一個整體被分成數等分或類別後的相對大小，例如其中一個等分或類別的多寡、不同等分或類別間的相對差異。

雖然比率、比例和百分比很常出現在日常生活中，但它們的用法卻也很常被混淆。如果用法不正確，很可能讓讀者產生誤解，甚至被有心人士利用，作為欺騙讀者的不實陳述。下面將簡單地介紹社會統計學裡比率、比例和百分比的差別，並舉例來說明每一種的數值呈現方法。

• 比率
• 比例
• 百分比
• 百分比和次數

比率

比率（ratio）可用來比較兩個或數個部分的相對大小，也稱為比或比值。舉例來說，在一門社會學的課程裡共有50位修課的學生，其中A班的學生人數為30人、B班的學生人數為20人，此時可以說A、B兩班的學生人數比為30比20，更簡單地說，為3比2。

比率最常用冒號來呈現兩數量之間的關係，例如上面A、B兩班的人數比可用3：2來表示，讀作3比2。另外，利用比率來表現兩個數量間的關係時，可以選擇哪一個數量放在前面，例如兩班的人數比也可以用B班和A班的人數比2：3來呈現，只是習慣上會把較大的數量放在前面。

再舉個例子，料理時常須要調配醬汁，食譜可能寫醬油2大匙、味醂1大匙，這代表醬油和味醂的比率為2比1，也就是說醬油的量為味醂的2倍。此外，比率是可擴增的，醬油2大匙和味醂1大匙也可擴增成醬油4大匙和味醂2大匙，只要兩個數量間維持著2比1的比率即可。

比例

比例（proportion）是指一個部分或一個數字和整體間的相對關係，會介於數值0和1之間。比例最常用來比較一個數字和總數，例如上面社會學課程裡兩個班級的學生人數若用比例來表現，可用下面的陳述方式：

• A班的學生占所有修課學生人數的比例為 。
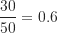• B班的學生占所有修課學生人數的比例為 。

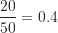再舉一個例子，假設在2022年家庭暴力的總通報件數為155000件，其中親密伴侶暴力有69750件、兒童虐待有24800件，若用比例來呈現這兩種虐待類型，可用下面的描述方法：

• 親密伴侶暴力案件占所有家庭暴力案件的比例為 。
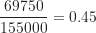• 兒童虐待案件占所有家庭暴力案件的比例為。

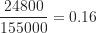藉由比例可以很清楚地看出一個數字占整體的大小，但比例通常會轉換成百分比，是更常看到的一種書面上表現方法。

百分比

比例可用百分比（percentage）來呈現，若要把比例轉換成百分比，只須把比例乘以100。以上面社會學課程裡兩個班級的學生人數比例來看，若改以百分比來呈現，可用下面的陳述方式：

• A班的學生占所有修課學生人數的百分比為 。
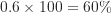• B班的學生占所有修課學生人數的百分比為 。

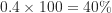有時候為了瞭解兩個數量在不同時間點的變化，可先計算出比例的改變，再轉換成百分比的改變。舉例來說，假設在2021年的兒童虐待案件有24000件，在2022年有25200件，那麼兒童虐待案件成長了多少？因為2022年的件數較2021年多，所以比例是增加的，首先計算增加的比例：

   

計算結果指出兒童虐待案件的增加比例為0.05，把這個增加比例乘以100，，即變成增加的百分比。也就是說，從2021年到2022年兒童虐待案件的成長率為5%。

再舉個例子，如果在2021年親密伴侶暴力案件數為75000件，在2022年為69750件，試問從2021年到2022年親密伴侶暴力案件的成長率是多少？

   

計算結果顯示成長率為-7%，由於有負號，代表是負成長。也就是說，和2021年相比較，2022年的親密伴侶暴力案件減少了7%。

百分比是一種很實用的相對數量的表現方式，特別是在兩個數量比較的時候。單從數字本身可能很難看出端倪，甚至可能讓人誤解，若將數字轉換成百分比後再做比較，將更能理解數字蘊含的訊息，下面來探討百分比和次數間的關係。

百分比和次數

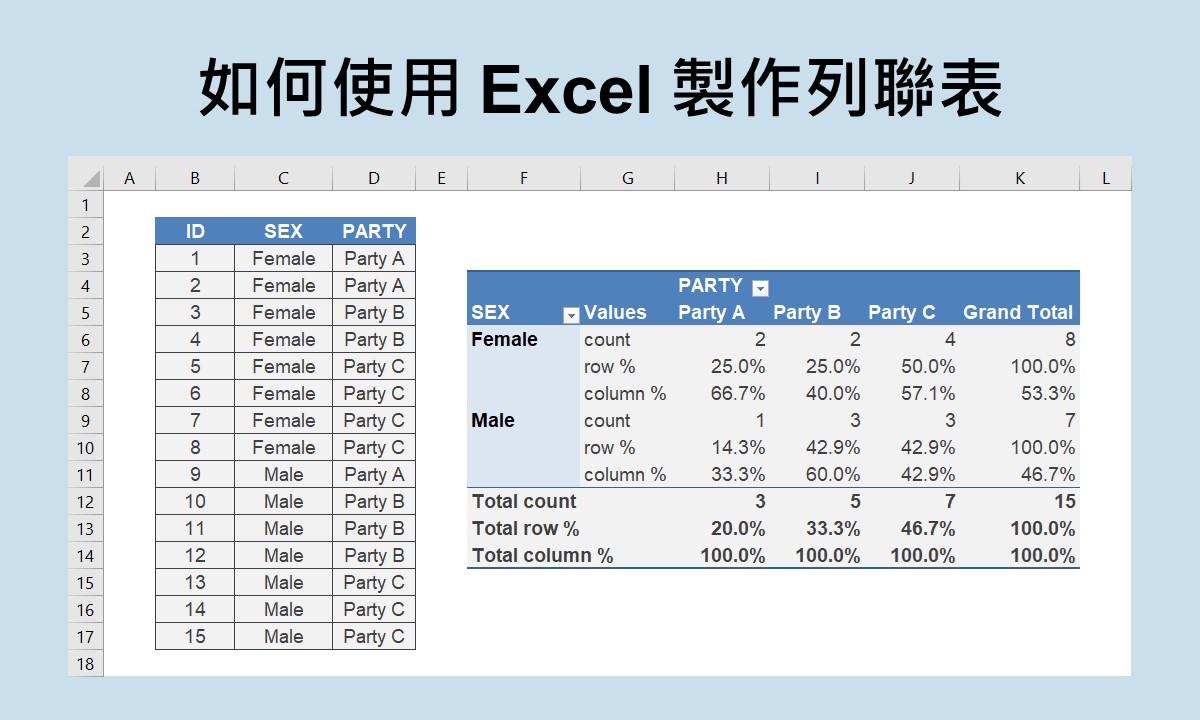
描述統計很常利用次數來呈現一個變項裡各個類別的分布情形，例如次數分配、分組分數次數分配。若要瞭解兩個變項之間的關係，有時會製作列聯表（或稱為交叉表），讓每一種類別的發生次數可以清楚地呈現出來。不過，光看次數本身很容易產生誤解，最好將次數轉換成百分比後再解釋，才能更確實地呈現實際的情況。

舉例來說，有一位政治學者想瞭解生理性別和政黨支持傾向之間的關係，在資料蒐集完成後，他製作了如下的列聯表來呈現這兩個變項間的關係。若單從每個類別的次數來看，不論是政黨Ａ或政黨Ｂ，支持者似乎都是生理男性多於生理女性。

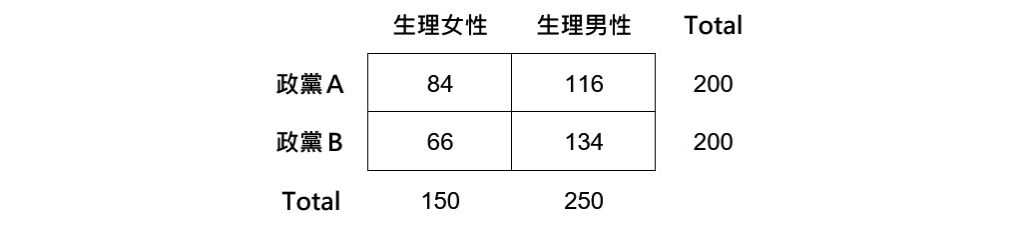
但若仔細觀察，會發現樣本裡的生理女性人數少於生理男性人數。此時，如果依據生理性別，分別計算出生理女性支持兩個政黨的百分比和生理男性支持兩個政黨的百分比，就可更清楚地看出生理性別和政黨支持傾向間的關係。

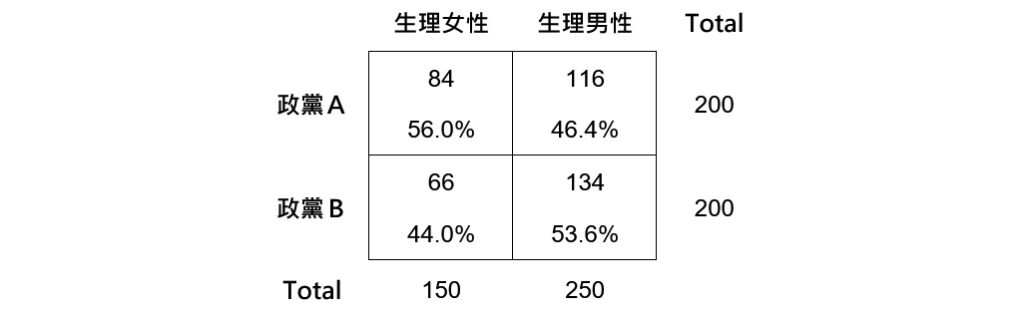
從上表可看出，傾向政黨Ａ的生理女性占了56.0%（），傾向政黨Ａ的生理男性則占了46.4%（）。雖然次數上看起來是生理男性比生理女性更傾向於支持政黨Ａ，但實際上傾向於支持政黨Ａ的生理女性百分比高於生理男性。

這個例子告訴我們單純看次數本身可能會造成誤解，必須考量總數，將次數轉換成百分比後再進行兩個數量的比較，才能真正地瞭解資料傳達的訊息。至於這兩個變項間的關係是否達到統計上顯著，則有賴假設檢定，若您有興趣瞭解，請參考卡方獨立性檢定的假設檢定。

以上為本篇文章對比率、比例和百分比的介紹，希望透過本篇文章，您瞭解了比率、比例和百分比各自的意義和使用時機，也學會了它們的計算方法。

若您喜歡本篇文章，請將本網站加入書籤，作為您的學習資源，並持續回訪本網站喔！另外，您也可以在Facebook和Twitter上找到我們喲！