效果量的意義和測量

研究人員透過研究的執行來解答研究問題，而各種統計檢定的假設檢定，即是用來評估變項之間是否有顯著的關聯性或自變項是否具有效果的一個過程。不過假設檢定的結果雖然可以看出變項間的關聯性或一個自變項的效果是否達到統計上的顯著（significant），卻無法顯示效果的大小。

有些人認為獲得某一特定檢定統計量的機率（ $p$ 值）或檢定統計量本身可作為效果大小的判斷標準，例如 $p$ 值愈小或檢定統計量愈大代表一個自變項的效果愈強。但這些並不是正確的概念， $p$ 值或檢定統計量皆不是衡量自變項效果大小的指標，唯有計算效果量（effect size），或稱為效應值，才能夠正確地評估統計分析結果的效果大小。

因此，不論是研究人員操縱的變項（自變項）或兩變項之間的關聯程度，為了測量一個效果的大小，就必須計算效果量。簡單地說，效果量是指自變項效果大小或變項間關聯程度的一種客觀、標準化的測量方法。以下將介紹效果量的用途和常見的效果量測量方式，包括Cohen´s d和皮爾森積差相關係數r。

效果量的用途
效果量的測量：Cohen´s d
- 變異不相等時Cohen´s d 的計算
- Cohen´s d 效果量的解釋
效果量的測量：皮爾森積差相關係數r

效果量的用途

資料分析時各種統計檢定的假設檢定過程中，會計算出檢定統計量和獲得該特定檢定統計量的機率值（ $p$ 值），再評估拒絕或保留虛無假設，也就是研究結果是顯著或不顯著。對於顯著的研究結果，通常為自變項或相關性，可進一步計算效果量來瞭解效果的大小。

效果量是一個客觀且標準化的數值，類似標準分數（z score）的概念。除了瞭解一個自變項的效果大小或變項間的關聯程度外，效果量還具有下面的3個用途：

跨研究的比較：因為效果量是一個標準化的數值，所以可以進行跨研究的比較，即使各個研究使用不同的測量尺度。不少科學研究會在相同的理論基礎上檢驗類似的研究假設，或複製先前的研究在不同的樣本數或樣本群體上，但沒有任一研究會主張研究結果百分之百的正確。為了瞭解相似研究的平均發現，即可利用每一個研究的效果量來進行單一的分析，稱為統合分析或後設分析（meta-analysis）。
統計檢定力的計算：顯著水準（α水準）、統計檢定的方向性、樣本大小和效果量皆和檢定力相互關聯，因此只要有α水準、檢定的方向性、樣本數和效果量等資訊，就可計算出檢定力。關於檢定力的詳細說明，請參考統計檢定力的意義和影響因素。

例如檢定力分析軟體G*Power，若要計算單一樣本ｔ檢定的檢定力，在Input Parameters方框中選擇Tail(s)（檢定的方向），再輸入Effect size d（效果量）、α err prob（α水準）和Total sample size（樣本大小），即可計算出Power (1-β err prob)（檢定力），請見下圖。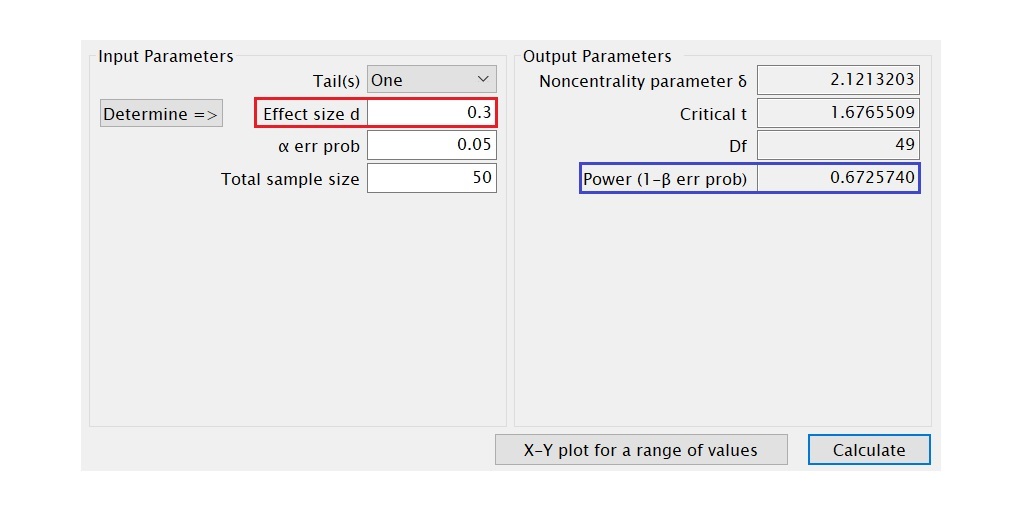
研究所需樣本數的計算：此點和第2點的檢定力計算相關聯。由於α水準、檢定的方向性、樣本大小、效果量和檢定力之間關係緊密，只要知道其中的4項資訊，即可求得最後一項資訊。因此，若有α水準、檢定的方向性、預期的效果量和研究欲達到的檢定力等資訊，即可計算出研究所需的樣本數。當研究具備足夠的樣本數時，愈能夠拒絕一個錯誤的虛無假設。

以單一樣本ｔ檢定為例，若使用檢定力分析軟體G*Power來計算達到檢定力0.80時所需要的樣本數，可在Input Parameters方框中選擇Tail(s)（檢定的方向），再輸入預期的Effect size d（效果量）、α err prob（α水準）和欲達到的Power (1-β err prob)（檢定力），即可計算出樣本大小，請見下圖。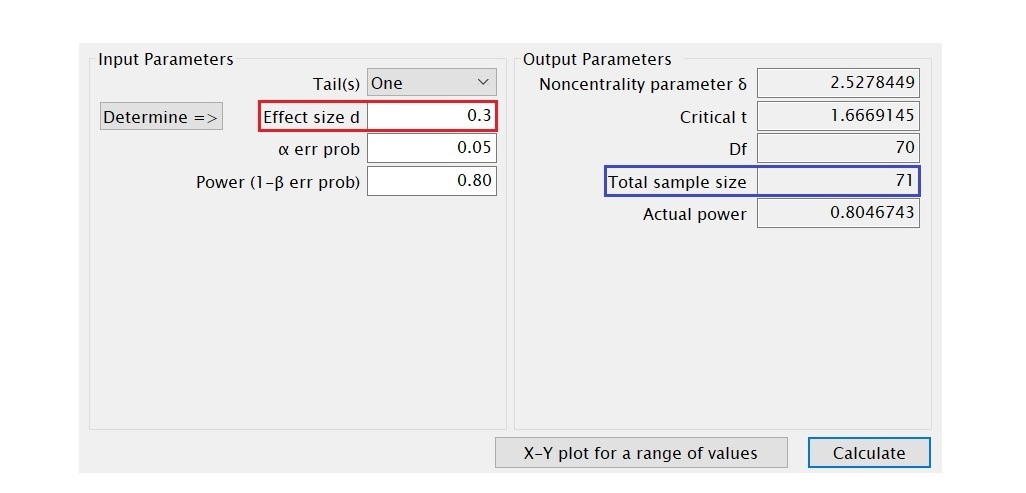

效果量的測量方法有許多種，最常見到和使用的有3種：Cohen´s d、皮爾森積差相關係數r、勝率比（odds ratio）。勝率比通常會在卡方檢定（chi-square test）或邏輯式迴歸分析（logistic regression）裡使用到，關於勝率比在卡方檢定裡的運用方法請參考卡方獨立性檢定的效果量：勝率比。下面將介紹Cohen´s d 和皮爾森積差相關係數這兩種效果量測量的方法。

效果量的測量：Cohen´s d

Cohen（1988）提出一個簡單地測量效果量的方法，以用來比較平均數的ｔ檢定而言，他發現效果量的大小和平均數之間的距離有很大的關聯。也就是說，若有兩個母群體平均數， $\mu_0$ 和 $\mu_1$ ，當 $\mu_1-\mu_0$ 的差值愈大的時候，效果量也愈大。

探討效果量時，通常是想瞭解效果的「大小」而不是效果的「方向」，所以可忽略數值的正負號。為了得到正數的 $\mu_1-\mu_0$ ，可取絕對值，變成 $\left | \mu_1-\mu_0 \right |$ 。接著，為了讓效果量標準化，可採取類似標準分數的計算方式，將平均數差值的絕對值除以母群體平均數，公式如下：

$d=\frac {\left | \mu_1-\mu_0 \right |}{\sigma}$

以單一樣本ｔ檢定為例，平均數之間的距離指樣本平均數和一個已知的母群體平均數之間的距離，也就是 $\overline X-\mu$ 。概念上，其效果量的公式為：

$d=\frac {\left | \overline X-\mu \right |}{\sigma}$

但在ｔ檢定裡，因為母群體標準差未知，所以改用樣本標準差來估計。此時，Cohen´s d 的估計值改用 $\hat d$ 來表示，單一樣本ｔ檢定的效果量計算公式也變成：

$\hat d=\frac {\left | \overline X-\mu \right |}{s}$

$\begin{equation*}\begin{CJK*}{UTF8}{bsmi}\begin{align*}\hat d &= \text {$d$ 的估計值} \\\overline X &= \text {樣本平均數} \\\mu &= \text {母群體平均數} \\s &= \text {樣本標準差}\end{align*}\end{CJK*}\end{equation*}$

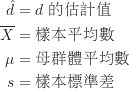
由於分子取絕對值的關係，所以不論 $\overline X > \mu$ 或 $\overline X < \mu$ ，計算出來的 $\hat d$ 皆會是正數。舉例來說，假設樣本平均數 $\overline X$ 為68、母群體平均數 $\mu$ 為72、樣本標準差 $s$ 為7，則單一樣本ｔ檢定的效果量為：

$\hat d=\frac {\left | \overline X-\mu \right |}{s}=\frac {\left | 68-72 \right |}{7} \approx 0.57$

不過這裡有一點須注意的地方，若採用有方向性的對立假設（ $H_1$ ），當 $\overline X-\mu$ 的結果和對立假設所描述的方向不同時，即應保留虛無假設（ $H_0$ ），也不用再去計算效果量。一般而言，會是在拒絕虛無假設時，也就是研究結果顯著的情況下，才有計算效果量的意義。

變異不相等時Cohen´s d 的計算

上面提到的Cohen´s d 的計算適用在單一樣本或兩個樣本具有相同變異（標準差）的情況下，若兩個樣本的變異不相等時，則有兩種計算方式的選擇。

第1種方法是使用控制組或基準（baseline）組別的標準差。若是實驗研究，研究人員會操縱自變項，而變項的操縱通常不只會改變平均數也可能會改變分數的分布狀態。因此，對於原本群體的分布狀態而言，使用控制組或基準組別的標準差會是較正確的估計值。

第2種方法是使用合併標準差估計值，此種方法適用在兩個群體彼此獨立的情況下，例如獨立樣本ｔ檢定。合併標準差估計值考量了樣本大小，並運用自由度（degrees of freedom）加權兩個樣本的變異數估計值。讓 $s_p$ 代表合併標準差估計值、 $n_1$ 為第1個樣本的樣本數、 $n_2$ 為第2個樣本的樣本數、 $s_1^2$ 為第一個樣本的變異數估計值、 $s_2^2$ 為第2個樣本的變異數估計值， $s_p$ 的公式為：

$s_p=\sqrt {\frac {(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

以獨立樣本ｔ檢定而言，假設第1個樣本的平均數為 $\overline X_1$ 、第2個樣本的平均數為 $\overline X_2$ ，若兩個樣本的變異不相等，則效果量Cohen´s d 的估計值 $\hat d$ 的計算公式如下：

$\hat d=\frac {\left | \overline X_1-\overline X_2 \right |}{s_p}=\frac {\left | \overline X_1-\overline X_2 \right |}{\sqrt {\displaystyle \frac {(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}}$

舉例來說，假設第一個樣本的平均數 $\overline X_1$ 為2、標準差 $s_1$ 為1.5、樣本數 $n_1$ 為10，第2個樣本的平均數 $\overline X_2$ 為4、標準差 $s_2$ 為2、樣本數 $n_2$ 為10，則獨立樣本ｔ檢定的效果量為：

$\begin{align*}\hat d &= \frac {\left | \overline X_1-\overline X_2 \right |}{\sqrt {\displaystyle \frac {(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}} \\&=\frac {\left | 2-4 \right |}{\sqrt {\displaystyle \frac {(10-1)(1.5)^2+(10-1)2^2}{10+10-2}}} \\& \approx 1.13\end{align*}$

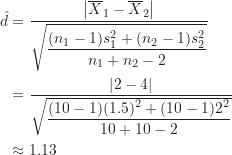
這裡計算出來的獨立樣本ｔ檢定的效果量為1.13，上面單一樣本ｔ檢定例子的效果量為0.57，雖然可明顯地看出1.13大於0.57，但要如何評估這些效果量的大小呢？以下來看看效果量的解釋。

Cohen´s d 效果量的解釋

從上面的內容可瞭解，當 $\hat d$ 的數值愈大代表效果量愈大，但到底多大的數值才能說是「大」的效果量呢？通常有兩種評估效果量大小的方法，第1種是對照已訂定的標準，第2種是對照在類似的研究領域裡過往的研究發現。

Cohen（1988）曾提供一個評估效果量大小的標準， $\hat d \leq 0.2$ 為小的效果量， $0.2<\hat d<0.8$ 屬於中等的效果量， $\hat d \geq 0.8$ 為大的效果量（見下表）。上面單一樣本ｔ檢定例子的效果量為0.57，以Cohen的標準來看，屬於中等的效果量；獨立樣本ｔ檢定例子的效果量為1.13，屬於大效果量。