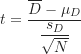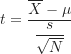🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
關聯樣本t檢定的假設檢定
關聯樣本t檢定(correlated samples t-test)是用來比較兩個相關聯的樣本或群組平均數是否有顯著差異的一種統計檢定方法,屬於一種母數檢定,而關聯樣本t檢定的假設檢定在檢驗第1個關聯樣本來自的母群體平均數等於第2個關聯樣本來自的母群體平均數之虛無假設。
關聯樣本也稱為相關樣本、配對樣本(matched samples)、成對樣本(paired samples)或相依樣本(dependent samples),而關聯樣本t檢定也很常被稱為成對樣本t檢定。這種統計檢定方法通常用在重複量數設計(repeated-measures design)或配對組設計(matched-group design)的研究設計上,是實驗設計裡很常使用到的統計檢定方法之一。
因為兩樣本之間具有關聯性,所以檢定統計量的計算不是使用原始分數(raw scores),而是配對的差值分數來進行分析,又稱為直接差分法(direct difference method)。這種方法將原本屬於兩組樣本的分析轉換成單一樣本的分析,換句話說,關聯樣本t檢定可看成是平均數差值的單一樣本t檢定。
由於本篇文章牽涉到假設檢定的過程,若您不清楚或不熟悉假設檢定,建議您可先閱讀假設檢定的步驟和範例,將有助於下面內容的理解。以下將先介紹關聯樣本的研究設計,再說明關聯樣本t檢定的檢定統計量公式和假設檢定的步驟,並舉例說明,最後再示範利用 SPSS 執行關聯樣本t檢定的操作方法。
關聯樣本的研究設計
關聯樣本(或稱為相關樣本、配對樣本、成對樣本或相依樣本)的研究設計是指樣本之間或群組之間並非各自獨立,而是具有關聯性,也不用隨機分配研究參與者(或稱為受試者)至實驗裡的不同情境。這種研究設計通常可分為兩種類型,一種是重複量數設計,另一種則是配對組設計,以下分別介紹。
重複量數設計
重複量數設計有時也稱為受試者內設計(within-subjects design)或前後測設計(before-after design),是指相同的受試者參與兩種或兩種以上的實驗情境。在這種研究設計裡,因為受試者本身即是實驗過程中的控制條件,所以可降低個人差異所導致的誤差,反而更能偵測到實驗裡自變項的效果。
舉例來說,若有位社會工作者想探討親密伴侶暴力防治宣導課程的效果,她在課程開始前請參與的學員填寫一份與課程內容相關的知識問卷,課程結束後再請學員們填寫一次問卷。這位社工應可預期每位學員的表現相對地前後一致,也就是前測成績不錯的學員,後測的成績也會不錯,而且大多數的學員成績在宣導課程結束後可能都有進步,使得前測和後測的成績間具有關聯性。
因為研究人員可以測量這層由相同學員所造成的前、後測成績之間的關聯性,所以在統計分析時可以移除這層關聯性,也可說是控制了研究裡的一個變異,藉此增加宣導課程(自變項)確實具備效果的可能性。
不過重複量數設計有一個很大的缺點,就是轉移效應(carryover effect)。轉移效應是指第一次測驗影響到第二次測驗的結果,尤其是當研究人員使用標準化測驗的時候,受試者可能會記得問題和答案,進而造成第二次測驗結果的偏誤。若轉移效應確實嚴重地影響到研究的信度,下面介紹的配對組設計可能會是較合適的研究設計。
配對組設計
配對組設計指研究人員透過和依變項相關的其他變項的測量,把測量結果相似的受試者進行配對,再隨機分配每一配對裡的其中一人至一個實驗情境、配對裡的另一人至另一個實驗情境。
舉例來說,若社會工作者相信學員的生理性別、教育程度和之前參與類似宣導課程的次數會影響親密伴侶暴力防治宣導課程的效果,因此利用這3個變項將學員進行配對。具備類似特質者配成一對,例如生理女性、高中教育程度和從未參與過類似課程的2位學員為一對,生理男性、大學教育程度和參與過1次類似課程的2位學員為另一對。
配對完成後,社會工作者將每一配對的其中一人隨機分配至親密伴侶暴力防治宣導課程組,配對裡的另一人則至通識教育課程組。課程結束後,每人皆填寫一份親密伴侶暴力防治的相關問卷,再比較兩組的成績是否有顯著的不同,藉此探討親密伴侶暴力防治課程是否具有效果。
配對組設計的優點是確保兩群組具有類似的特質,而且和重複量數設計一樣,能夠測量配對受試者之間的關聯性並在統計分析時移除該變異。另外,這種研究設計不會有轉移效應的問題,是個滿常被使用的關聯樣本的研究設計。
關聯樣本t檢定的檢定統計量公式
依據變異數總和法則(variance sum law),在兩個獨立樣本的設計裡,樣本平均數差異抽樣分配的變異等於兩樣本各自的平均數抽樣分配的變異數之總和:
![]()
由於標準誤(標準差)是變異數的平方根,所以樣本平均數差異抽樣分配的標準誤如下:
![]()
當母群體變異數未知的時候,會利用樣本變異數 ![]() 來估計母群體變異數
來估計母群體變異數 ![]() ,則樣本平均數差異的標準誤估計值如下:
,則樣本平均數差異的標準誤估計值如下:
(1) ![]()
不過,實際上樣本平均數差異的標準誤估計值的通式為下面的公式:
(2) ![]()
上面的公式(2)中,![]() 、
、![]() 分別指從第1個和第2個母群體裡抽取出來的樣本平均數抽樣分配標準誤的估計值,
分別指從第1個和第2個母群體裡抽取出來的樣本平均數抽樣分配標準誤的估計值,![]() 是指兩個樣本或群組間的相關係數。在獨立樣本的設計裡,因為兩個樣本各自獨立,沒有關聯性,所以
是指兩個樣本或群組間的相關係數。在獨立樣本的設計裡,因為兩個樣本各自獨立,沒有關聯性,所以 ![]() ,使得
,使得 ![]() ,樣本平均數差異標準誤的估計值才會是上面公式(1)的樣子。
,樣本平均數差異標準誤的估計值才會是上面公式(1)的樣子。
但在關聯樣本的設計裡,因為兩個樣本或群組具有關聯性,所以 ![]() 須保留在公式裡。因此,概念上關聯樣本t檢定的檢定統計量公式為:
須保留在公式裡。因此,概念上關聯樣本t檢定的檢定統計量公式為:
(3) 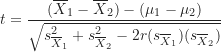
不過,利用公式(3)來進行運算的過程會有點複雜,所以還有一種計算上較友善且能夠得到和公式(3)一樣結果的方法稱為直接差分法。這種方法利用各個配對分數的差值進行運算,將原本屬於兩個樣本的檢定變成單一樣本的檢定。
若讓 ![]() 代表配對的差值分數,
代表配對的差值分數,![]() 為樣本差值分數的平均數,
為樣本差值分數的平均數,![]() 為母群體差值分數的平均數,
為母群體差值分數的平均數,![]() 為樣本差值分數的標準差,
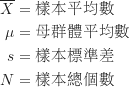
為樣本差值分數的標準差,![]() 為差值分數的總個數(或樣本配對分數的組數),關聯樣本t檢定的檢定統計量為:
為差值分數的總個數(或樣本配對分數的組數),關聯樣本t檢定的檢定統計量為:
(4) 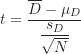
樣本差值分數的平均數實際上為兩個樣本平均數(![]() 和
和![]() )的差值,也就是
)的差值,也就是 ![]() 。為了運算上的方便,讓
。為了運算上的方便,讓 ![]() 指所有樣本差值分數的平方和、
指所有樣本差值分數的平方和、![]() 指所有樣本差值分數總和的平方,公式(4)可再變成下面的運算公式:
指所有樣本差值分數總和的平方,公式(4)可再變成下面的運算公式:
(5) 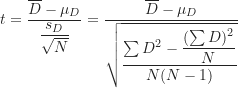
關聯樣本t檢定和單一樣本t檢定的檢定統計量公式相當類似(請見下表),兩者的差別在於單一樣本t檢定使用原始數據而關聯樣本t檢定使用配對的差值分數來進行分析。
| 關聯樣本t檢定 | 單一樣本t檢定 |
|---|---|
|
|
|
|
|
|
瞭解了關聯樣本t檢定的檢定統計量公式來由以及其與單一樣本t檢定的檢定統計量差異後,接下來探討關聯樣本t檢定的假設檢定過程。
關聯樣本t檢定的假設檢定
關聯樣本t檢定用來探討兩個相關聯的樣本或群組的平均數是否有顯著的不同,更簡單地說,是在評估自變項是否帶有效果。若用上面提到的配對差值分數的概念來看,這種檢定方法用來評估母群體差值分數平均數 ![]() 的虛無假設(
的虛無假設(![]() ),又因為
),又因為 ![]() ,所以也可說是評估
,所以也可說是評估 ![]() 的虛無假設。
的虛無假設。
研究人員須依據研究目的、理論基礎和過往的研究發現來擬定研究假設,而不是憑空臆測。研究假設又可分為無方向性和有方向性的假設,若是有方向性的假設,須在對立假設(![]() )裡明確地闡明方向,例如前測的平均數低於後測的平均數。
)裡明確地闡明方向,例如前測的平均數低於後測的平均數。
研究假設擬定好後,再考量研究的性質、目的以及研究可能帶來的後果,選擇合適的顯著水準或稱為α水準,習慣上為0.05、0.01或更嚴苛的0.001。然後,再根據研究假設的方向性之有無,決定假設檢定為雙尾檢定或單尾檢定。
關聯樣本t檢定使用t分配和t檢定統計量,而t檢定統計量的計算公式即為上面的公式(5)。由於在大多數的情況下,研究人員是評估 ![]() 的虛無假設,所以公式(5)可再簡化為下面的公式:
的虛無假設,所以公式(5)可再簡化為下面的公式:
(6) 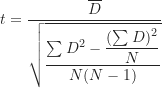
求得t檢定統計量後,查詢t分配表,依據自由度(degrees of freedom,簡寫為df)和事先選擇好的α水準,找到相對應的臨界值。關聯樣本t檢定的自由度為 ![]() ,其中
,其中 ![]() 是指配對差值分數的總個數(或樣本配對分數的組數)。最後,運用檢定統計量和臨界值比較的決策規則來評估研究結果,此時須區分成雙尾檢定和單尾檢定兩種情況:
是指配對差值分數的總個數(或樣本配對分數的組數)。最後,運用檢定統計量和臨界值比較的決策規則來評估研究結果,此時須區分成雙尾檢定和單尾檢定兩種情況:
- 雙尾檢定:在對立假設裡沒有指出兩個關聯樣本平均數差異的方向,當t檢定統計量的絕對值等於或大於臨界值的絕對值時,可以拒絕虛無假設,接受對立假設。
- 單尾檢定:在對立假設裡指出兩個關聯樣本平均數差異的方向,須先確認平均數差異的方向是否和對立假設所述的方向一致,若不一致,直接保留虛無假設,無須再比較t檢定統計量和臨界值。若方向一致,當t檢定統計量的絕對值等於或大於臨界值絕對值時,可以拒絕虛無假設。例如對立假設描述後測成績會高於前測成績,如果描述統計量顯示後測平均成績低於前測平均成績,則直接保留虛無假設。
如果是使用統計分析軟體,例如 SPSS、SAS,通常會輸出獲得特定t檢定統計量的機率(![]() 值)而非臨界值。此時須使用機率比較的決策規則,當
值)而非臨界值。此時須使用機率比較的決策規則,當 ![]() 時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
時,即可拒絕虛無假設,接受對立假設;反之,則保留虛無假設。
關聯樣本t檢定和其他的母數檢定的統計檢定方法一樣,樣本資料須滿足特定的假設後才可使用,以下簡單地說明這些假設。
關聯樣本t檢定的基本假設
關聯樣本t檢定是對樣本來自的母群體做出特定假設的母數檢定(parametric test),所以執行假設檢定時,樣本資料須滿足特定的條件。因為關聯樣本t檢定類似於單一樣本t檢定,所以樣本資料須符合的假設也和單一樣本t檢定相同。
簡單地說,關聯樣本t檢定要求樣本配對差值分數平均數 ![]() 的抽樣分配須呈現常態分配,為了達到該要求,配對差值分數的總個數須等於或大於30,或樣本來自的母群體分數本身即為常態分配。
的抽樣分配須呈現常態分配,為了達到該要求,配對差值分數的總個數須等於或大於30,或樣本來自的母群體分數本身即為常態分配。
另外,變項資料的測量尺度須至少為等距尺度,才能使用關聯樣本t檢定。若變項的測量尺度為次序尺度,或資料沒有滿足常態分配的要求時,關聯樣本t檢定便不再合適,此時可改用符號檢定或 Wilcoxon 配對符號等級檢定。
瞭解了關聯樣本t檢定的基本假設和假設檢定的步驟後,以下將舉一個例子示範關聯樣本t檢定假設檢定的操作過程。
關聯樣本t檢定假設檢定的範例
假設有一位社會工作者想探討家庭暴力防治課程是否影響學員的知識程度,他設計了一份家庭暴力相關的知識問卷,共20題選擇題。他在課程開始前請10位參與學員填寫該份問卷,課程結束後再請學員填寫一次相同的問卷,這10位學員的前測(pre-test)與後測(post-test)成績如下表所示。使用α水準0.05、雙尾檢定,試問家庭暴力防治課程是否影響了學員對該議題的知識程度?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| pre-test | 9 | 14 | 17 | 7 | 15 | 11 | 16 | 12 | 13 | 10 |
| post-test | 6 | 15 | 20 | 11 | 17 | 13 | 18 | 15 | 17 | 16 |
這位社會工作者想瞭解家庭暴力防治課程是否「影響」學員的知識程度,屬於無方向性的研究假設,所以對立假設和虛無假設分別為:
- 對立假設(
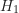 ):家庭暴力防治課程對學員的知識程度有影響,也就是說,這10位學員的前後測差值分數平均數是來自於母群體差值分數平均數
):家庭暴力防治課程對學員的知識程度有影響,也就是說,這10位學員的前後測差值分數平均數是來自於母群體差值分數平均數 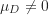 的一組隨機樣本。
的一組隨機樣本。 - 虛無假設(
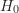 ):家庭暴力防治課程對學員的知識程度沒有影響,也就是說,這10位學員的前後測差值分數平均數是來自於母群體差值分數平均數
):家庭暴力防治課程對學員的知識程度沒有影響,也就是說,這10位學員的前後測差值分數平均數是來自於母群體差值分數平均數 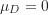 的一組隨機樣本。
的一組隨機樣本。
這位社會工作者選擇0.05的顯著水準(![]() ),且因為研究假設不具有方向性,所以採用雙尾檢定。若用符號來表示,可寫成
),且因為研究假設不具有方向性,所以採用雙尾檢定。若用符號來表示,可寫成 ![]() 。
。
由於前測和後測為相同的參與學員,為關聯樣本裡的重複量數設計,且研究目的在於前測和後測成績的比較,所以可使用關聯樣本t檢定來檢驗前測和後測的成績是否有顯著的不同。
關聯樣本t檢定使用t分配和t檢定統計量,利用上面的公式(6)來計算t檢定統計量,先將套用公式所需要的數值在如下的表格裡計算出來。
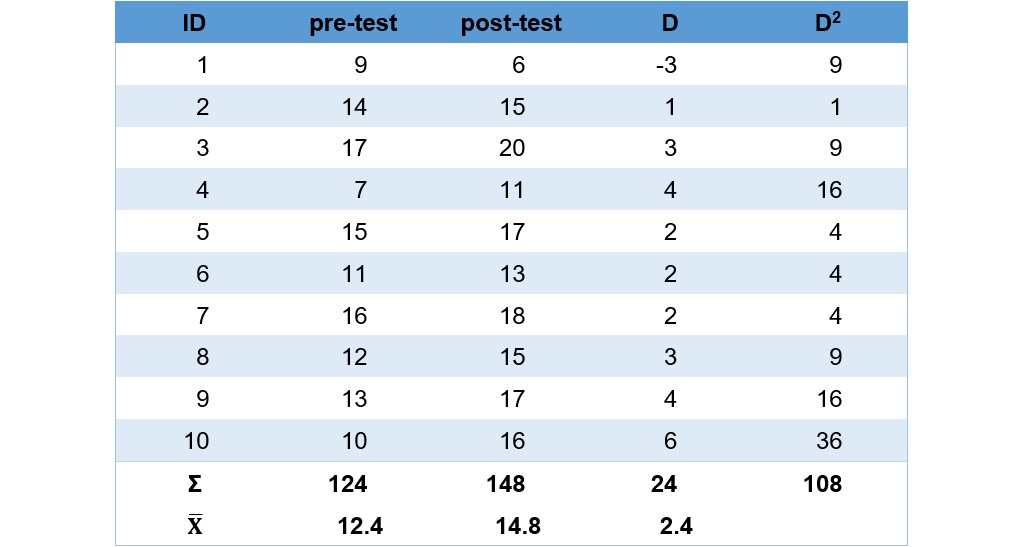
上表中的 ![]() 指前後測成績的差值,這裡是用後測成績減去前測成績,反之亦可。再將上表中的數值帶入公式(6)裡,計算過程如下:
指前後測成績的差值,這裡是用後測成績減去前測成績,反之亦可。再將上表中的數值帶入公式(6)裡,計算過程如下:
![Rendered by QuickLaTeX.com \[ t=\frac {\overline D}{\sqrt {\dfrac {\sum D^2-\dfrac {(\sum D)^2}{N}}{N(N-1)}}}=\frac {2.4}{\sqrt {\dfrac {108-\dfrac {24^2}{10}}{10 \times 9}}}=\frac {2.4}{\sqrt {0.56}} \approx 3.207 \]](https://drfishstats.com/wp-content/ql-cache/quicklatex.com-65bdd73e8c7adf252a51827b416952b0_l3.png)
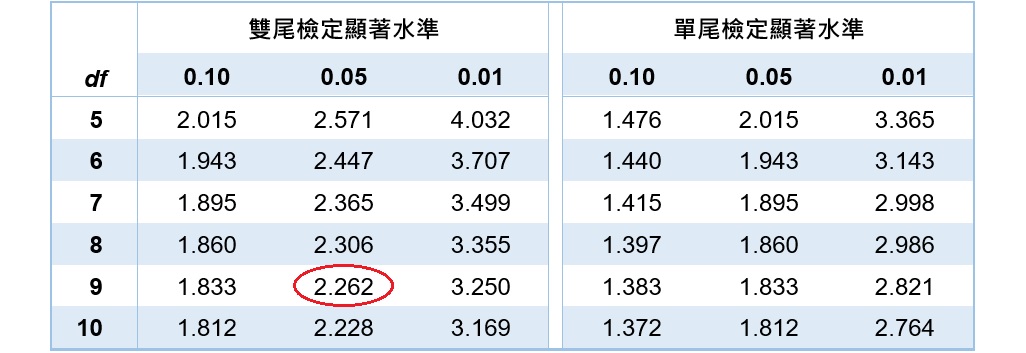
計算結果得到t檢定統計量為3.207,而自由度為 ![]() 。然後,查詢t分配表,當雙尾檢定且
。然後,查詢t分配表,當雙尾檢定且 ![]() 時,t臨界值為
時,t臨界值為![]() 。
。
最後,運用t檢定統計量和臨界值比較的決策規則,因為 ![]() ,所以拒絕虛無假設,接受對立假設。關聯樣本t檢定的分析結果指出,家庭暴力防治課程對學員的知識程度有影響,再進一步查看前測和後測的平均成績,學員在後測的平均成績(
,所以拒絕虛無假設,接受對立假設。關聯樣本t檢定的分析結果指出,家庭暴力防治課程對學員的知識程度有影響,再進一步查看前測和後測的平均成績,學員在後測的平均成績(![]() )明顯地高於前測的平均成績(
)明顯地高於前測的平均成績(![]() )。
)。
當檢定結果達到統計上顯著,也就是分析結果指出自變項帶有效果時,可以再進一步計算信賴區間來探討樣本平均數差值可能存在的數值範圍,也可以計算效果量來瞭解自變項的效果大小。若您想深入瞭解這些內容,請參考關聯樣本t檢定的信賴區間和效果量。
運用 SPSS 執行關聯樣本t檢定
將上面範例中10位學員的前測和後測的成績輸入至 SPSS 資料編輯器中,變項名稱分別設為 PRE 和 POST。輸入完成後,點選功能表的分析 » 比較平均數 » 成對樣本T檢定,帶出「配對樣本T檢定」視窗。關於 SPSS 的資料輸入方法,請參考 SPSS 操作環境和資料輸入。
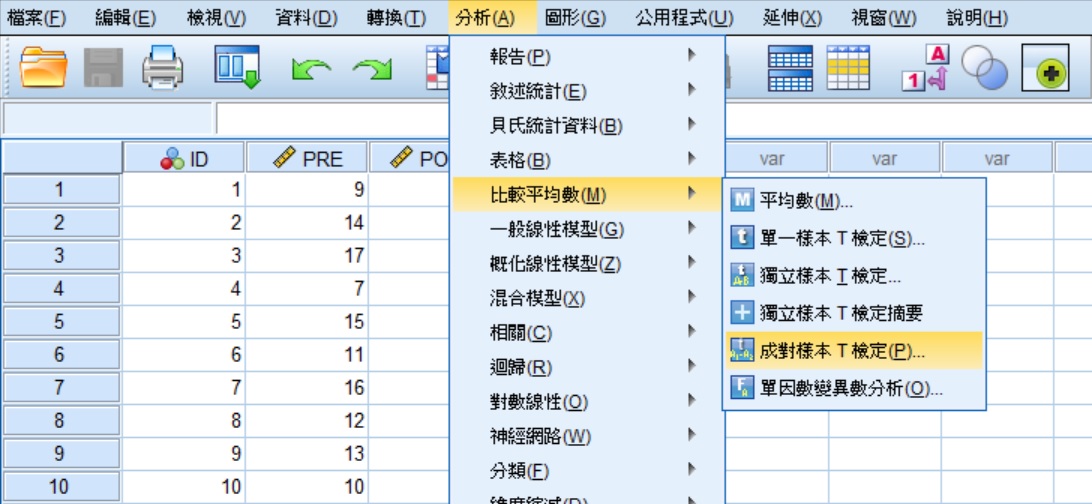
在「配對樣本T檢定」視窗中,將變項 PRE 移至變數1的位置、變項 POST 移至變數2的位置,可以使用變項清單方框旁的箭頭進行移動或使用滑鼠直接拖曳。
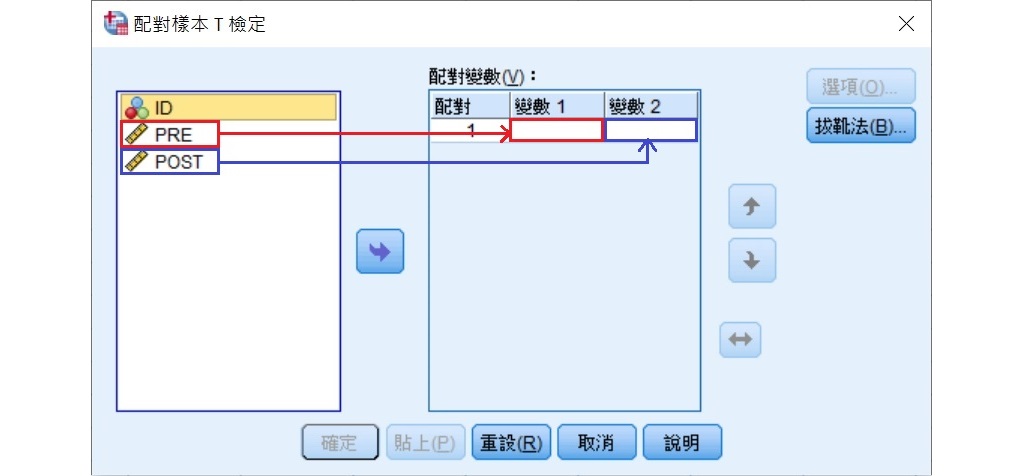
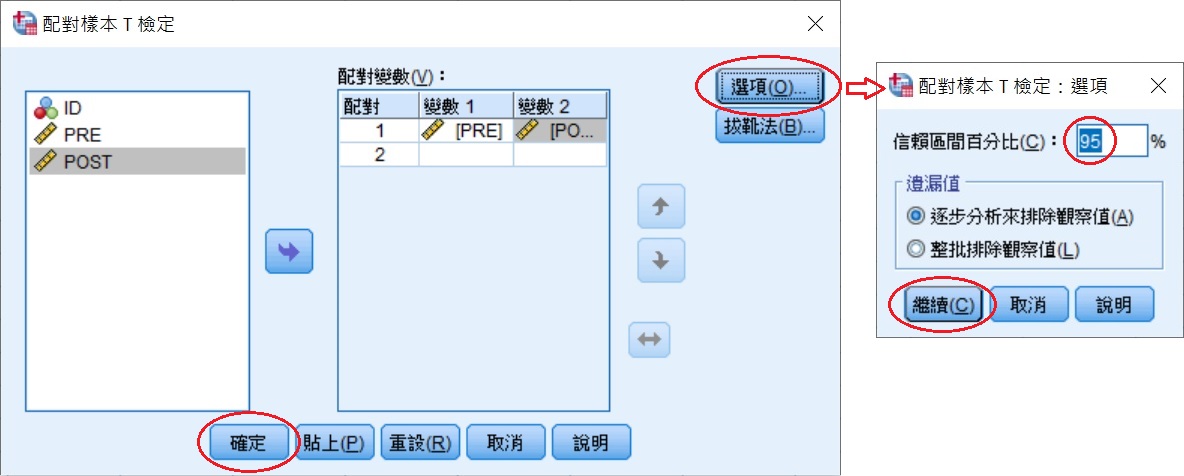
將 PRE 和 POST 移到配對變數(V)方框裡的位置後,點選視窗最右邊的選項(O),帶出「配對樣本T檢定:選項」小視窗。
依據設定好的α水準,在信賴區間百分比(C)的方格中填入相對應的數值。這個範例的 α 水準為0.05,所以在方格中填入95;若 α 水準為0.01,則填入99,以此類推。完成後,點選繼續(C),回到上一視窗後,再點選確定。
SPSS 會輸出3個表格:成對樣本統計量表、成對樣本相關性表和成對樣本檢定表。第1個「成對樣本統計量」表為變項 PRE 和 POST 的描述性統計量,從下表可看出,前測的平均數為12.4、標準差為3.204;後測的平均數為14.8、標準差為3.994。

第2個表格為「成對樣本相關性」表,顯示兩個變項 PRE 和 POST 之間的關聯程度和方向。從該表格可以看出,前測和後測成績之間的皮爾森積差相關係數為0.806,表示兩者之間具有正向的高度相關性。
此外,顯著性(![]() 值)為0.005,由於
值)為0.005,由於 ![]() ,代表前後測之間有顯著的關聯性,也就是當前測的成績愈高的時候,後測的成績也愈高。關於皮爾森積差相關係數假設檢定的詳細介紹,請參考皮爾森積差相關係數的假設檢定。
,代表前後測之間有顯著的關聯性,也就是當前測的成績愈高的時候,後測的成績也愈高。關於皮爾森積差相關係數假設檢定的詳細介紹,請參考皮爾森積差相關係數的假設檢定。

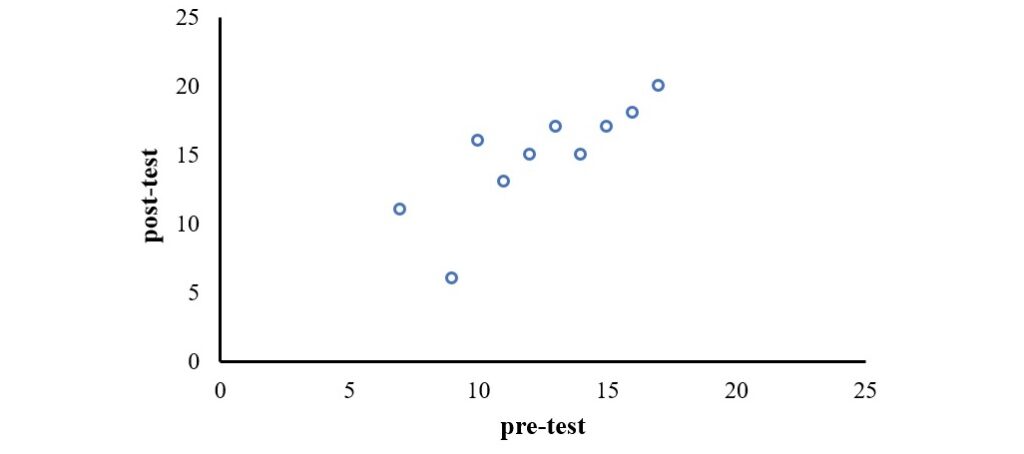
若將前測成績 PRE 置於橫座標軸、後測成績 POST 置於縱座標軸,繪製一如下圖的散布圖,可以明顯地發現當前測成績提升的時候,後測的成績也跟著提升。此外,點和點之間的分布頗為緊密,代表前後測成績之間的關聯程度很高。
最後一個表格為「成對樣本檢定」表,也就是假設檢定的結果。從下表可以看出,前後測差值分數的平均數 ![]() 為-2.4,t檢定統計量為-3.207,在自由度為9的情況下,雙尾顯著性為0.011。運用機率比較的決策規則,因為
為-2.4,t檢定統計量為-3.207,在自由度為9的情況下,雙尾顯著性為0.011。運用機率比較的決策規則,因為 ![]() ,所以拒絕虛無假設,接受對立假設。關聯樣本t檢定的分析結果顯示,家庭暴力防治課程影響了學員的知識程度,後測的成績明顯地高於前測的成績。
,所以拒絕虛無假設,接受對立假設。關聯樣本t檢定的分析結果顯示,家庭暴力防治課程影響了學員的知識程度,後測的成績明顯地高於前測的成績。

SPSS 的運算是用前測減去後測的成績,所以計算出來的配對差值分數平均數 ![]() 和t檢定統計量皆為負數,不同於上面範例中紙筆計算的正數結果。雖然符號不同,但數值沒有改變,也不會影響分析的結果。不過,在討論研究發現或撰寫研究報告時,仍須注意前測和後測各自的平均數,才能做出正確的敘述。
和t檢定統計量皆為負數,不同於上面範例中紙筆計算的正數結果。雖然符號不同,但數值沒有改變,也不會影響分析的結果。不過,在討論研究發現或撰寫研究報告時,仍須注意前測和後測各自的平均數,才能做出正確的敘述。
關聯樣本t檢定適用在兩個「關聯的」群組或樣本平均數的比較,如果兩個群組或樣本間彼此獨立、不具關聯性,兩者平均數的比較則須使用獨立樣本t檢定。若您想進一步瞭解關聯樣本t檢定和獨立樣本t檢定之間的差異,可參考獨立樣本和關聯樣本t檢定的比較。
以上為本篇文章對關聯樣本t檢定的介紹,希望透過本篇文章,您瞭解了關聯樣本的研究設計類型與關聯樣本t檢定的假設檢定過程,也學會了利用 SPSS 執行關聯樣本t檢定的操作方法。若您喜歡本篇文章,請將本網站加入書籤,並持續回訪本網站喔!另外,也歡迎您追蹤本網站的 Facebook 和/或 X(Twitter)專頁喲!
如果您覺得本篇文章對您有幫助,歡迎買杯珍奶給 Dr. Fish!小小珍奶,大大鼓勵,您的支持將給 Dr. Fish 更多撰寫優質文章的動力喔!