🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
變項之間關係的基本特色
變項之間的關係(correlation)是指變項間關聯的程度和方向,通常在執行更深入的推論統計分析之前,除了次數分配、平均數、標準差、偏態等描述統計的探討之外,也會瞭解變項之間的關聯程度和方向。關於各個描述統計主題的介紹,可參考描述統計下的各篇文章。
變項之間有多種不同的關聯型態,而不同測量尺度的變項間更有不同的相關分析方法,請參考測量尺度和相關係數的選擇。但在瞭解較為艱澀的相關分析技術前,本篇文章先介紹3個變項間關係的基本特色,分別為線性關係(linear relationship)、關係的方向、完全關係和不完全關係。若您只對文章的某部分內容感興趣,也可以點選下方的連結,即可直接跳至您想閱讀的內容。
線性關係
線性關係是指兩個變項之間的關係可以用一條直線來呈現,通常可從一個變項(X)來預測另一個變項(Y)的改變。但並非所有變項間的關係都是線性關係,也有可能是曲線關係(curvilinear relationship)。曲線關係的兩個變項在一開始可能為同時增加或減少的趨勢,但到了某一個點之後,兩者之間的關係就改變了方向,屬於一種非線性關係(nonlinear relationship)。
這層關係可以透過兩個變項的散布圖(scatter plot)來觀察,也就是成對的兩個變項的觀察數值繪製而成的圖形。上面提到的曲線關係,若從散布圖來看,應會呈現U或倒U的形狀。詳細的散布圖繪製方法,可以參考如何繪製散布圖。
舉一個例子來看,若X變項為每週讀統計學的時間、Y變項為期中考的成績,下表為5位學生在這兩個變項的資料:
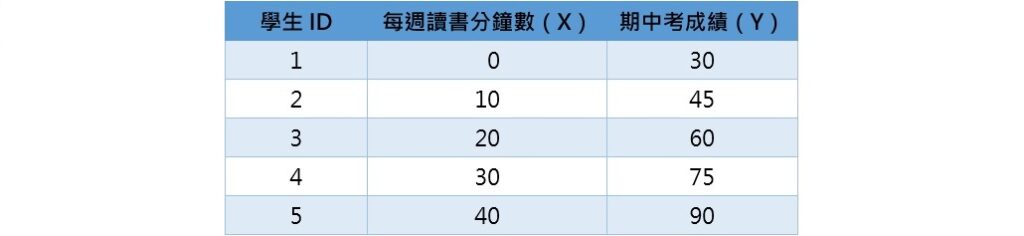
先製作一散布圖,觀察每週讀書的分鐘數和期中考成績之間的關係。用5位學生的資料所繪製出的散布圖如下,從該圖可看出每週的讀書時間愈多,期中考成績愈高。
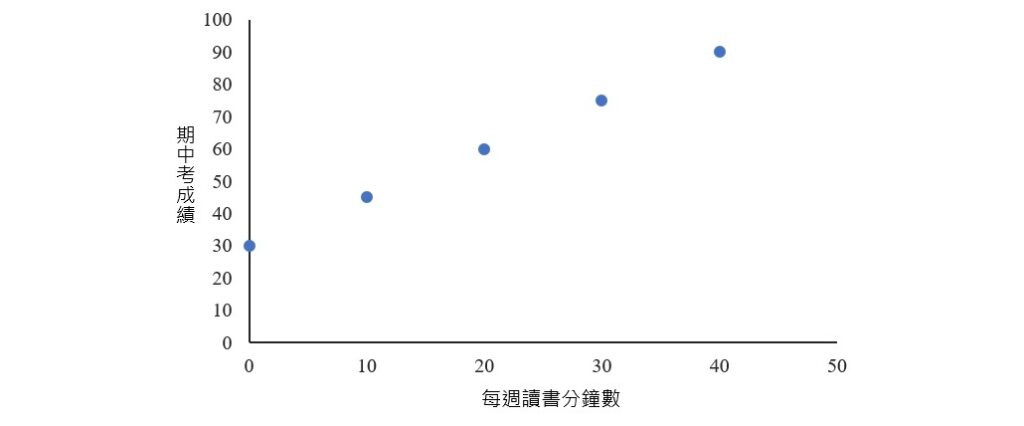
從上圖還可看出,這5位學生的資料所構成的5個點很完美地落在一條直線上,如下圖所示。而當一條直線可以用來描述兩個變項之間的關係時,這兩變項之間的關係即稱為線性關係。
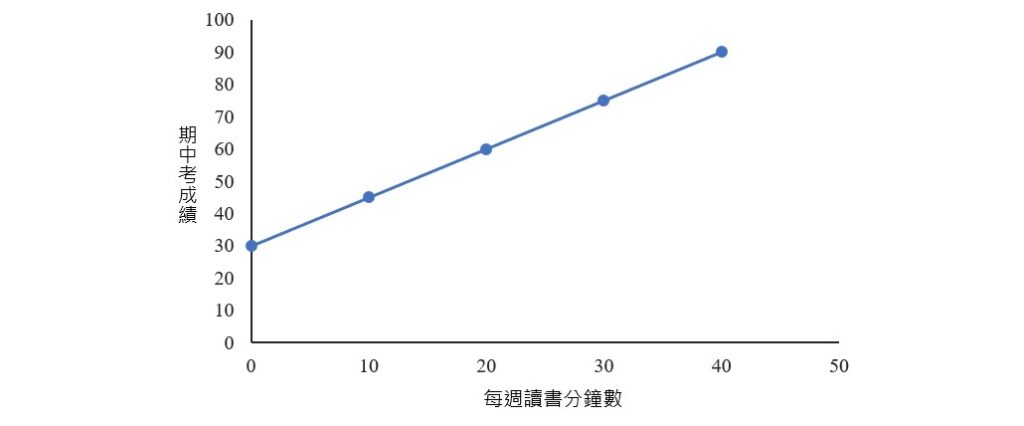
上圖中那一條能夠完美地穿越散布圖上所有點的直線可以用一條直線方程式來呈現:
![]()
這條直線方程式裡的![]() 指Y的截距(intercept),
指Y的截距(intercept),![]() 指直線的斜率(slope),下面來看這兩者的意義和計算方式。
指直線的斜率(slope),下面來看這兩者的意義和計算方式。
截距
Y的截距是指,當X等於0的時候Y的值,也就是直線和縱座標軸(Y軸)相交的地方。以上面5位學生的資料來看,Y的截距![]() 為30。
為30。
斜率
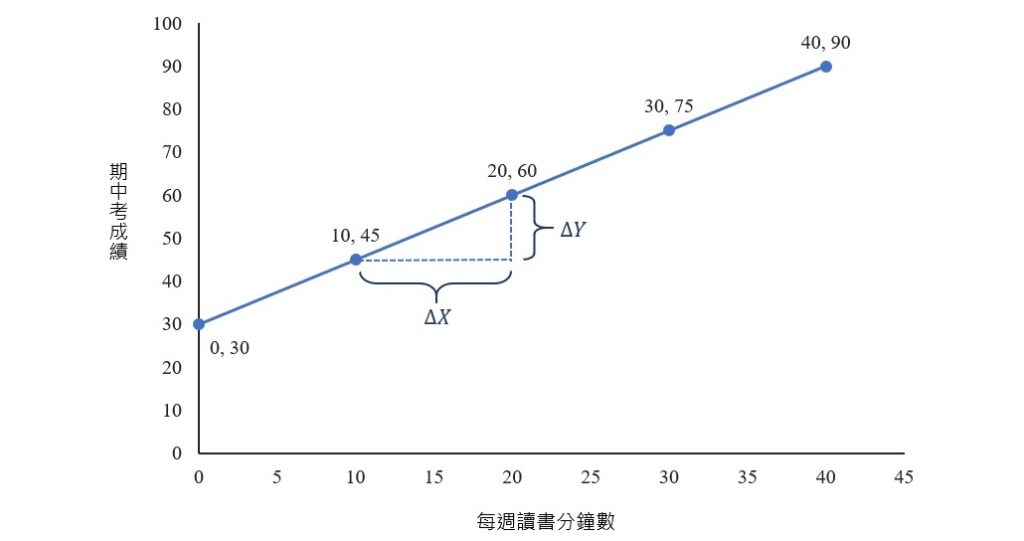
直線的斜率是變化率的測量,指當X改變1個單位的時候Y所改變的數值。因為是直線,所以斜率是常數,可以從直線上的任何兩個點來計算。公式如下:
![]()
其中![]() 、
、![]() 為任2個
為任2個![]() 的觀察值,
的觀察值,![]() 、
、![]() 則為
則為![]() 、
、![]() 相對應的
相對應的![]() 值。以上面5位學生的例子而言,用第2位和第3位學生的資料來計算,斜率
值。以上面5位學生的例子而言,用第2位和第3位學生的資料來計算,斜率![]() 為:
為:
![]()
經過上述的計算過程,可得知5位學生的資料所建構出的直線方程式為![]() 。這直線方程式傳達的訊息如下:
。這直線方程式傳達的訊息如下:
- 若每週沒有花任何時間讀統計學,期中考成績為30分。
- 每當增加1分鐘的讀書時間,期中考成績會增加1.5分(斜率1.5的意義)。
- 當每週讀書的時間增加,期中考的成績也會提高。
此外,直線方程式還可作為預測用途。運用上面例題的直線方程式,若已知某位學生每週花15分鐘讀統計學,則這位學生的期末考成績為![]() 分。
分。
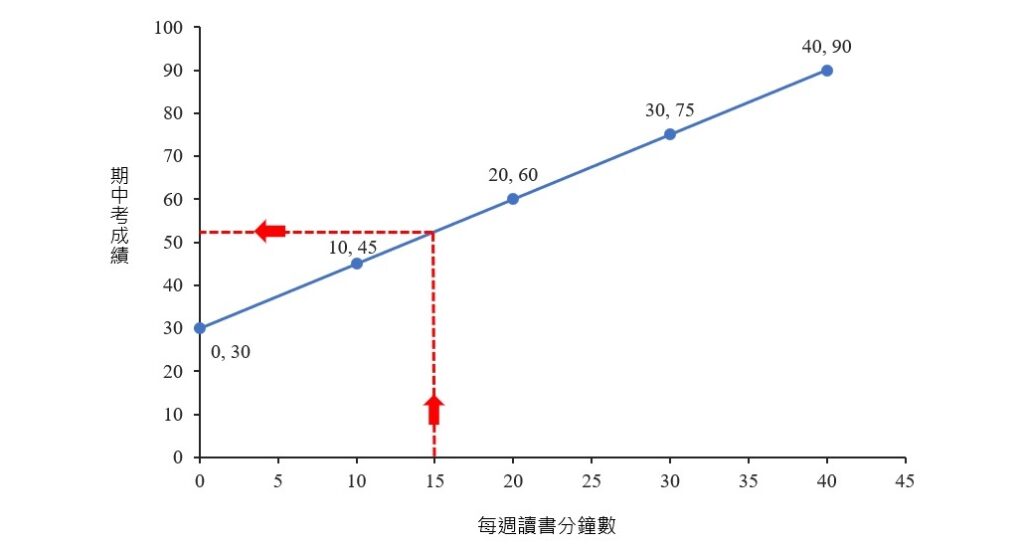
除了利用直線方程式外,也可以透過圖形來做預測,如下圖所示。從橫座標軸的15分鐘處,往上畫一條線至直線的相交處後,向左畫一條線,與縱座標軸交會的地方即為預測的期中考成績,和運用直線方程式計算出來的結果相同。
直線方程式裡的斜率![]() 還可用來瞭解變項間關係的方向,這也是變項間關係的第2個特性,接下來針對這個特性進行說明。
還可用來瞭解變項間關係的方向,這也是變項間關係的第2個特性,接下來針對這個特性進行說明。
正向關係和負向關係
上面提到的直線方程式中的斜率可以用來判斷兩變項之間關係的方向,若斜率為正數,代表兩變項之間的關係為正向關係(positive relationship);反之,若斜率為負數,則兩變項之間的關係為負向關係(negative relationship)。
所謂正向關係,表示當X的值增加的時候,Y的值也跟著增加,上面5位學生的資料和下圖皆為正向關係的例子。
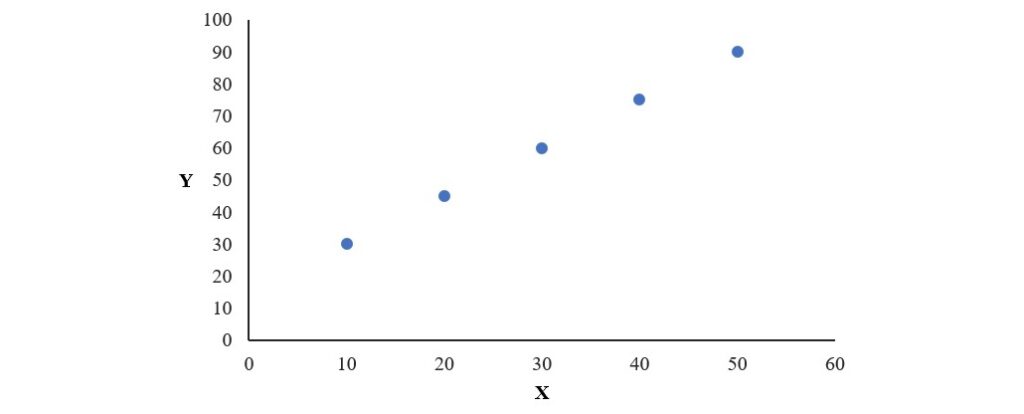
反過來看,負向關係表示當X的值增加的時候,Y的值減少,如下圖所示。
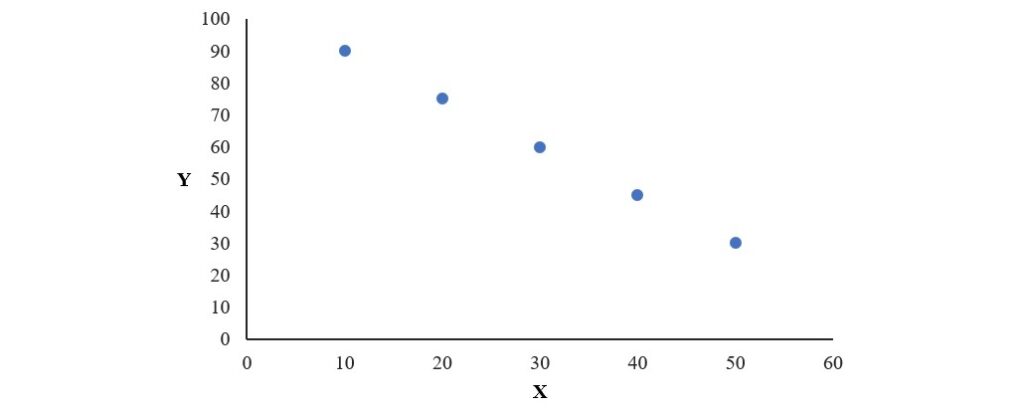
上面兩個圖裡面的點皆完美地落在一條直線上,但實際上研究人員蒐集到的資料通常不會如此完美地落在同一直線上,而是分散的狀態。若依據資料所構成的點是否完美地落在一直線上來看,變項間的關係還可分成完全關係和不完全關係,下面來說明。
完全關係和不完全關係
根據兩個變項的觀察數值所構成的點是否完美地落在同一條直線上,變項間的關係可分為完全關係(perfect relationship)和不完全關係(imperfect relationship)。
若兩變項成對的觀察數值能夠完美地被一條直線穿過,也就是散布圖上的每個點皆能完美地落在同一直線上,例如上面5位學生的資料,不論是正向關係或負向關係,皆稱為完全關係。
但現實生活中,很少資料屬於完全關係,特別是社會或行為科學領域的資料。當兩變項構成的點沒有完美地落在同一直線上,可是兩變項之間仍舊呈現出正向或負向關係的趨勢,且可畫出一條適合所有點的直線時,此種情況稱為不完全關係。
下圖即為不完全關係的散布圖和趨勢線。X變項和Y變項的觀察值所構成的點沒有完美地落在一條直線上,但是從散布圖可以看出當X的值增加的時候,Y值減少的負向關係趨勢,所以可以從中畫出一條適合所有點的直線。此時,X和Y變項之間稱為負向、不完全的線性關係。
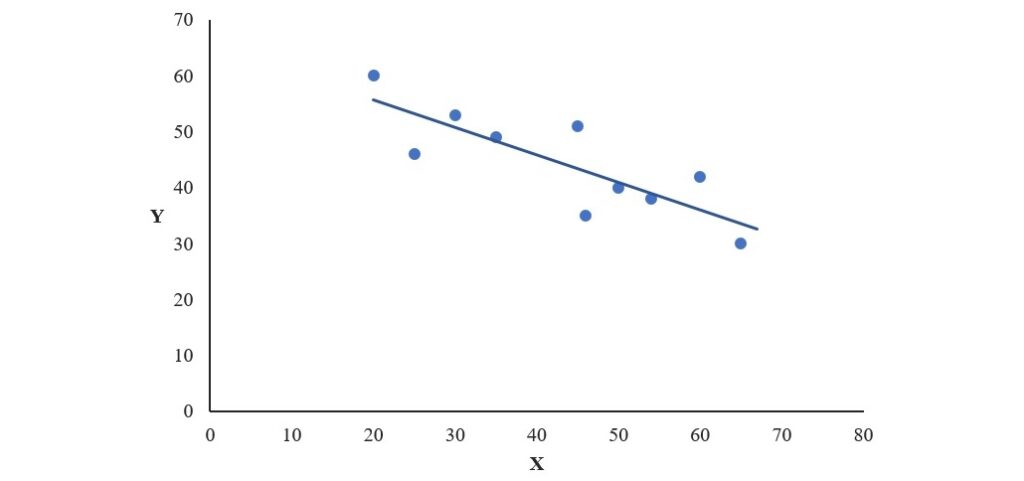
上圖中那條適合所有點的線稱為迴歸線(regression line),是根據最小平方法(least squares)準則,將預測誤差最小化後所建構出來的一條線,所以又稱為最小平方迴歸線。關於該條迴歸線的詳細說明,請參考最小平方迴歸線的建構和計算。
以上為本篇文章對變項之間關係的基本特色之介紹,希望透過本篇文章,您瞭解了線性關係和非線性關係、正向關係和負向關係、完全關係和不完全關係之間的區別,而對這些概念的認識將有助於相關分析的執行與分析結果的解釋。
若您喜歡本篇文章,請將本網站加入書籤,作為您的學習資源,並持續回訪本網站喔!另外,您也可以在Facebook和Twitter上找到我們喲!