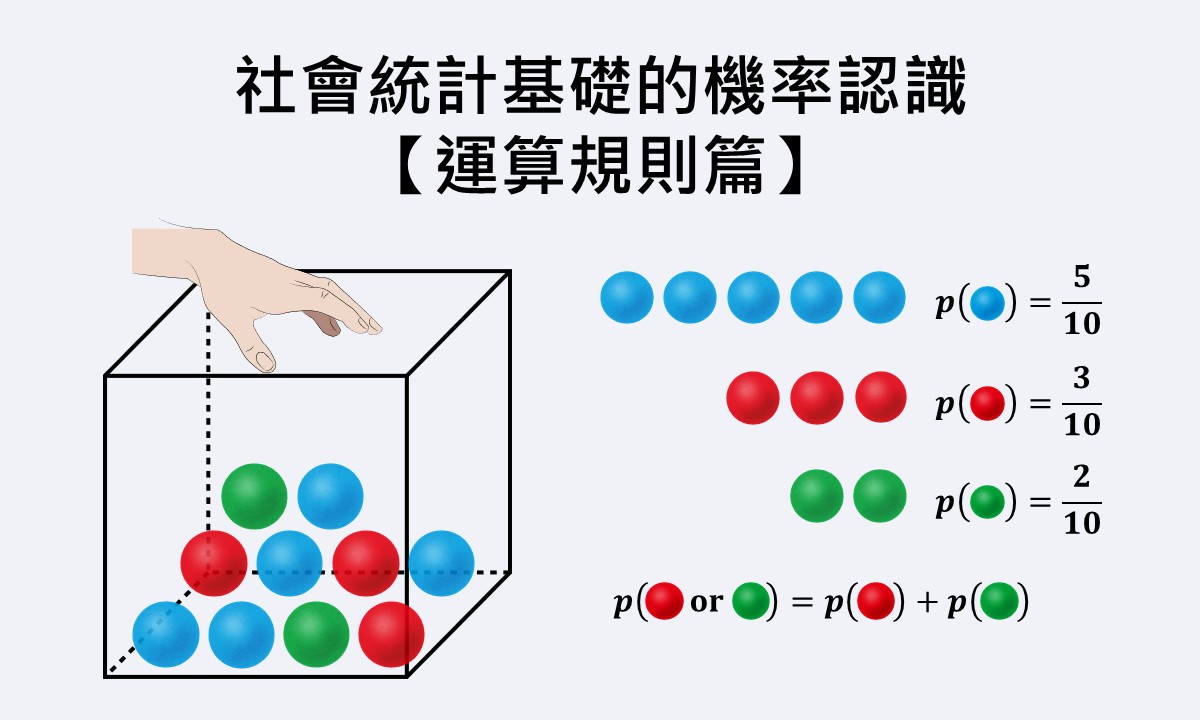
🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
研究假設的種類和寫法
社會研究是一個長期的過程,包含研究問題的提出、理論的探索和建構、研究假設的擬定、資料蒐集和整理、資料分析以及研究結果的討論等步驟,其中和社會統計最為相關的部分為研究假設的提出、資料蒐集和資料分析。
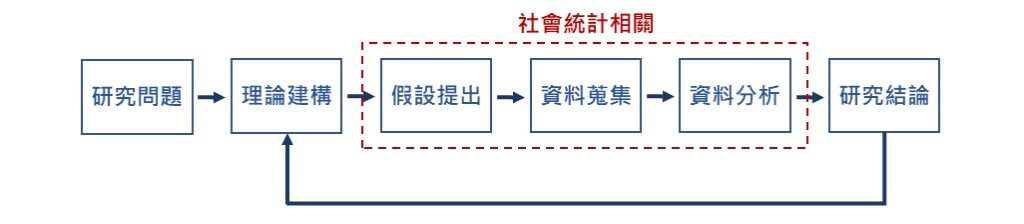
原則上,研究問題提出後,須探索和整理相關的研究發現與理論,並在此基礎上,明確地闡述研究假設(research hypothesis)。換句話說,研究假設的提出並非憑空揣測,而須具有理論的基礎。因此,研究執行的進程中,須先清楚地撰寫研究假設,再進入整體的研究設計和資料蒐集。
任何一種研究都會有兩種用來解釋研究結果的假設,稱為對立假設(alternative hypothesis)和虛無假設(null hypothesis),在最後的研究結果中僅能有一者為真實。以下將解釋這兩種研究假設的差異,並示範闡述方法,最後探討研究假設的方向性。
研究假設的種類
研究假設可以分為對立假設和虛無假設,這兩個假設必須互斥且周延(mutually exclusive and exhaustive),代表除了這兩個假設外,不會有其他的假設存在,而且只有一個假設能夠解釋最後的研究結果。
虛無假設
虛無假設用來主張自變項的效果不存在,所有的情境是相同的或無關聯的,通常用符號![]() 來表示。換句話說,虛無假設闡述研究結果裡組別之間不會因為自變項而有所不同,或變項間是相同的或不存在關聯性。每個研究都是在檢驗虛無假設,當研究結果指出虛無假設是錯誤的時候,研究人員即可拒絕虛無假設,並接受對立假設。
來表示。換句話說,虛無假設闡述研究結果裡組別之間不會因為自變項而有所不同,或變項間是相同的或不存在關聯性。每個研究都是在檢驗虛無假設,當研究結果指出虛無假設是錯誤的時候,研究人員即可拒絕虛無假設,並接受對立假設。
對立假設
對立假設是虛無假設的相反,用來主張自變項的效果存在,情境之間是不相同的或有關聯的,通常用符號![]() 來表示。換句話說,對立假設闡述研究結果裡組別之間所產生的差異是因為自變項的關係,或變項間是不相同的或存在關聯性。
來表示。換句話說,對立假設闡述研究結果裡組別之間所產生的差異是因為自變項的關係,或變項間是不相同的或存在關聯性。
研究假設的寫法
研究假設的擬定和闡述須具有理論基礎,不能憑空揣測或捏造。舉例來說,根據犯罪學的社會解組理論(social disorganization theory),當一個社區裡居民的流動率低且凝聚力強的時候,該區域的社會結構較健全,對犯罪的社會控制力量也較強。基於該理論,有位犯罪學者想探討守望相助隊的設立是否會影響社區的犯罪率,這研究的兩種假設的寫法分別為:
- 對立假設(
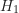 ):守望相助隊的設立會影響社區的犯罪率。
):守望相助隊的設立會影響社區的犯罪率。 - 虛無假設(
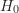 ):守望相助隊的設立不會影響社區的犯罪率。
):守望相助隊的設立不會影響社區的犯罪率。
不過,研究假設還可再區分為是否具有方向性,上面兩個假設為無方向性(non-directional)的寫法。若是有方向性(directional)的假設,須明確地指出自變項效果的方向,以下做進一步的討論。
研究假設的方向性
研究假設可再分為無方向性或有方向性的假設,若是無方向性的假設,通常會使用「會影響」、「有效果」、「有關聯」、「有所不同」等寫法,不會明確地指出影響或關聯的方向,例如上面的守望相助隊例子。當研究假設不具有方向性時,研究人員執行的統計檢定稱為雙尾檢定(two-tailed test)。
若是有方向性的假設,須在對立假設(![]() )中明確地闡述自變項效果的方向或變項間關係的方向,虛無假設(
)中明確地闡述自變項效果的方向或變項間關係的方向,虛無假設(![]() )則主張自變項不具有對立假設(
)則主張自變項不具有對立假設(![]() )所闡述方向的效果(代表自變項沒有效果或具有相反於對立假設所闡述方向的效果)。當研究假設具有方向性時,研究人員執行的統計檢定稱為單尾檢定(one-tailed test)。
)所闡述方向的效果(代表自變項沒有效果或具有相反於對立假設所闡述方向的效果)。當研究假設具有方向性時,研究人員執行的統計檢定稱為單尾檢定(one-tailed test)。
同樣以上面守望相助隊的例子來說明,若犯罪學者依據理論推測守望相助隊的設立會減少社區的犯罪率,則兩種假設的寫法分別為:
- 對立假設(
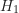 ):守望相助隊的設立會降低社區的犯罪率。
):守望相助隊的設立會降低社區的犯罪率。 - 虛無假設(
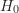 ):守望相助隊的設立不會降低社區的犯罪率。
):守望相助隊的設立不會降低社區的犯罪率。
此種虛無假設的寫法帶有兩種意涵:守望相助隊的設立不會影響社區的犯罪率或是會增加社區的犯罪率。從上述的寫法也可以看出,這兩種假設是互斥且周延,若其中一者是錯誤的,另一者必定為真實。
研究假設是否要有方向性須依據理論和過往的研究發現來決定,若有強力的證據支持研究結果會朝某特定的方向發展,可考慮使用有方向性的假設,不然仍應以無方向性的假設為主。下表為3種統計檢定的無方向性和有方向性研究假設的例子:
| 統計檢定 | 研究假設 | 無方向性 | 有方向性 |
|---|---|---|---|
| 皮爾森積差相關係數 | 變項間有關聯, | 變項間為正向關係, | |
| 變項間沒有關聯, | 變項間不為正向關係, | ||
| 單一樣本t檢定 | 樣本來自 | 樣本來自 | |
| 樣本來自 | 樣本來自 | ||
| 獨立樣本t檢定 | 兩樣本來自 | 兩樣本來自 | |
| 兩樣本來自 | 兩樣本來自 |
闡述完研究假設後,再透過資料的蒐集來評估虛無假設。若資料證實虛無假設是錯誤的,則可拒絕虛無假設,並接受對立假設。但嚴格來說,在研究結果裡,「拒絕」或「接受」研究假設的說法並不完全正確,而是應該說「若虛無假設為真實,則得到該資料數據的機率是多少」,這個概念將會被運用在推論統計中的各種假設檢定(hypothesis testing)上。
以上為本篇文章對於研究假設的種類和寫法的介紹,希望透過本篇文章,您瞭解了研究假設的種類,也學會了研究假設的撰寫方法。
若您喜歡本篇文章,請將本網站加入書籤,作為您的學習資源,並持續回訪本網站喔!另外,您也可以在Facebook和Twitter上找到我們喲!