🐟 請您尊重本網站的智慧財產權,如有任何引用,請註明出處:Dr. Fish 漫游社會統計。(文章發表日期)。文章名稱。文章網址
顯著水準和決策規則
行為或社會科學研究的執行是一連串的過程,為了能夠在統計分析的階段判斷研究的結果,在研究資料蒐集前須先提出研究假設和決定顯著水準(significance level),才能在資料分析時運用決策規則(decision rule)評估能否拒絕虛無假設。
研究假設包含虛無假設和對立假設,統計檢定的過程是在評估虛無假設,而這裡就牽涉到推論統計裡一個很關鍵的問題:到底要有多少的證據才能拒絕虛無假設?這個問題的答案即與顯著水準的選擇和決策規則的行使有關。
由於顯著水準的選擇為研究假設擬定後的步驟,若您不清楚或不熟悉研究假設的種類和闡述方法,建議您先閱讀研究假設的種類和寫法,將有助於以下內容的銜接和理解。下面將先介紹顯著水準的意義,再說明決策規則,最後解釋顯著水準和檢定方向性有無之間的關係。
顯著水準(α水準)的意義
執行統計分析時,會去評估虛無假設而非對立假設(alternative hypothesis),因為研究人員只能夠計算機遇事件(chance event)的機率,也就是自變項不具有任何影響時事件發生的機率,而無法計算對立假設的機率。換句話說,若虛無假設是真實的,在只有機會的影響之下,得到研究人員所蒐集到的數據結果之機率值(![]() 值)是多少。
值)是多少。
計算並得到數據結果的機率值之後,必須和一個數值相比較,才能夠決定要拒絕或保留虛無假設,而這個數值就是顯著水準,又稱為α水準(alpha level)。因此,顯著水準是指研究人員在資料蒐集前已經決定好、用來和分析結果的機率值相比較的一個機率數值,常見的數值為0.05、0.01或0.001,用符號表示為![]() 、
、![]() 或
或![]() 。
。
顯著水準可說是研究人員決定去拒絕虛無假設的信心程度,由於沒有人能夠斷言自己的研究結果百分之百正確,所以顯著水準也可被視為研究人員願意接受第一類型錯誤(拒絕一個真實的虛無假設)的機率值。關於判斷虛無假設真偽的過程中可能犯下的錯誤,請參考第一和第二類型錯誤的意義和關聯。
舉例來說,若將顯著水準設為0.05,代表將拒絕虛無假設的機率限制在0.05以內。也就是說,在只有機會的影響下,若分析結果的機率在100次當中等於或小於5次,研究人員才願意拒絕虛無假設並接受對立假設。這個就是評估研究結果的過程,即為下面探討的決策規則。
決策規則
研究假設分為虛無假設和對立假設,兩者互斥且周延,當其中一者為錯誤,另一者必定為真實,且沒有其他的可能性存在。擬定完研究假設後,研究人員設定顯著水準,決定在何種情況下能夠拒絕虛無假設。拒絕或保留虛無假設的決策規則如下:
- 若分析結果的機率
 ,拒絕虛無假設,接受對立假設。
,拒絕虛無假設,接受對立假設。 - 若分析結果的機率
 ,保留虛無假設。
,保留虛無假設。
另外一種可以評估研究結果的方法為檢定統計量和臨界值的比較,通常會在紙筆計算的過程中使用這種方法。這種方法須先計算出各種統計檢定方法的檢定統計量後,利用顯著水準、自由度等資訊查詢相應的臨界值表,找到臨界值後再比較檢定統計量和臨界值。
若是雙尾檢定,臨界值會有正、負兩個數值,決策規則為檢定統計量的絕對值等於或大於臨界值的絕對值時,可以拒絕虛無假設。若是單尾檢定,須先注意檢定統計量的數值是否和事先擬定的對立假設方向一致,如果一致,決策規則為檢定統計量的絕對值等於或大於絕對值時,拒絕虛無假設;如果不一致,則直接保留虛無假設。關於這種研究結果的評估方法,會在各種統計檢定的文章裡有更深入的說明和示範。
當研究人員拒絕虛無假設,接受對立假設時,此種研究結果稱為顯著(significant);若無法拒絕虛無假設,也就是必須保留虛無假設時,研究結果則稱為不顯著(non-significant)。分析結果達到統計上顯著並不是指研究結果很重要,而是代表研究結果不太可能是機遇或隨機事件,所以值得更多的研究去進一步探討和分析。
從決策規則可看出顯著水準的選擇會影響研究的結果,請見下表。若分析結果的機率為0.03,當顯著水準設為0.05時,因為![]() ,所以可拒絕虛無假設;但當顯著水準改設為0.01時,因為
,所以可拒絕虛無假設;但當顯著水準改設為0.01時,因為![]() ,則無法拒絕虛無假設。由此可知,0.01是一個比0.05更為嚴苛的顯著水準,因為研究人員較不容易拒絕虛無假設。
,則無法拒絕虛無假設。由此可知,0.01是一個比0.05更為嚴苛的顯著水準,因為研究人員較不容易拒絕虛無假設。

顯著水準的選擇並沒有黃金準則,通常會依據研究的性質、目的和錯誤結論可能造成的後果來決定。若一個研究為探索(exploratory)性質,目的在於初步瞭解一個議題,研究完成後再決定是否進行更深入的探討,可選擇較寬鬆的顯著水準;若一個研究為解釋(explanatory)性質,目的在於建立因果關係並推論至其他群體,因為錯誤的結論可能造成嚴重的後果,所以需要較嚴格的顯著水準。
顯著水準的選擇還須注意研究假設是否具有方向性,沒有方向性的統計檢定稱為雙尾檢定(two-tailed test),有方向性的統計檢定則稱為單尾檢定(one-tailed test),以下將進一步探討顯著水準和研究假設方向性之間的關係。
雙尾和單尾檢定
研究假設可區分為無方向性和有方向性的假設,若無方向性,通常會使用「會影響」、「有效果」或「有關聯」等寫法,例如興建社區活動中心會影響社區裡少年的犯罪率。若是有方向性的假設,則須在對立假設中明確地寫出自變項效果的影響方向,例如興建社區活動中心會降低社區裡少年的犯罪率。
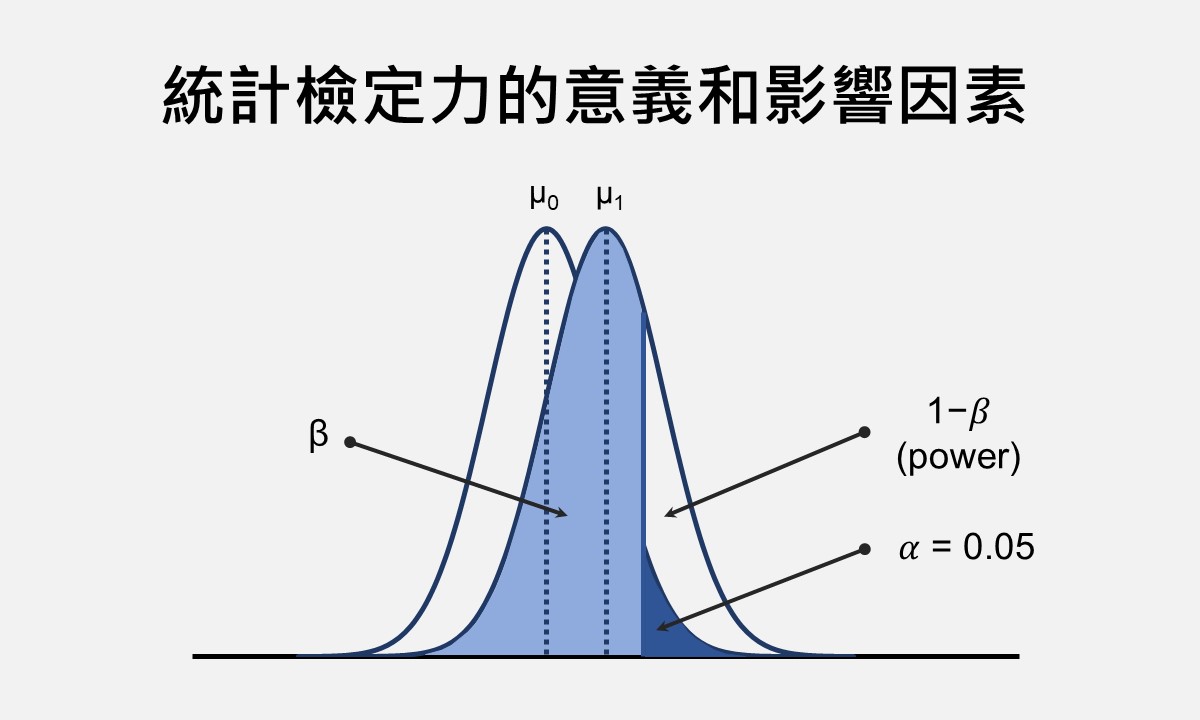
由於沒有方向性的研究假設不預測自變項效果的方向,所以顯著水準會平均地劃分在分配的兩側,若以0.05的顯著水準為例,一側各為0.025,如下圖左右兩側尾端的深藍色區域。依據上述的決策規則,研究分析結果在單側的機率必須等於或小於0.025,才可以拒絕虛無假設並接受對立假設。因為顯著水準會平均劃分在分配的兩端,所以無方向性的假設檢定稱為雙尾檢定。
若是有方向性的研究假設,依據假設所預測的方向,顯著水準會集中在分配的一側,例如下圖深藍色加淺藍色的區域。根據決策規則,研究分析結果的機率等於或小於0.5且與預測的方向相同時,即可拒絕虛無假設。由於顯著水準集中在一側,此種有方向性的假設檢定稱為單尾檢定。
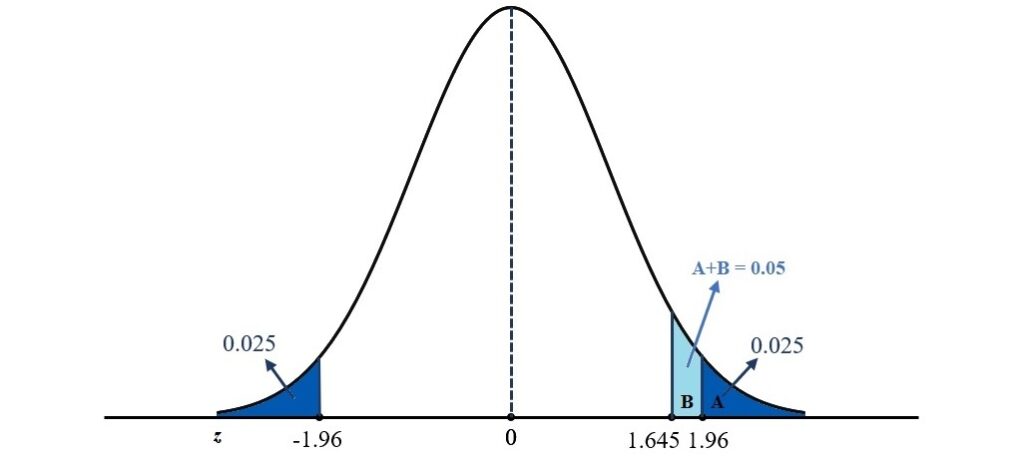
從上圖可以看出,顯著水準在單尾檢定的區域大於雙尾檢定的區域,使得拒絕虛無假設的可能性提高,也可能讓研究人員傾向於單尾檢定的使用。但若單尾檢定的研究結果顯示自變項的效果剛好跟預測的方向相反,由於此種情況無法拒絕虛無假設,所以可能錯失發現自變項效果的機會。
原則上,除非有下列的兩種情況,較適合使用單尾檢定外,建議所有的研究都儘量採取雙尾檢定的假設檢定方式:
- 即使研究結果和預測的方向完全相反,也會被視為沒有實際上的差別或助益,僅能導致保留虛無假設的結果(Ruxton & Neuhäuser,2010)。例如對立假設闡述興建社區活動中心會降低社區裡少年的犯罪率,但研究結果卻顯示社區活動中心的興建增加少年的犯罪率;由於興建社區活動中心非但沒有改善犯罪反而導致犯罪的增加,便沒有核准該項公共設施興建的意義存在。
- 有很強的理論基礎,且有相關的數據佐證,證明單尾檢定是適當的假設檢定方式。若研究結果和預測的方向完全相反,雖然最後還是只能保留虛無假設,但卻可藉此檢視理論與先前的研究發現。
此外,有些研究人員可能在看到研究結果後產生修改研究假設的衝動,例如單尾檢定改成雙尾檢定或雙尾檢定改成單尾檢定,但此種作法不僅違反研究程序,也會增加研究錯誤的機率。因此,研究人員不但需要在資料蒐集前設定好顯著水準,且決定好採用雙尾或單尾檢定,更需要將這些設定從一開始貫徹至研究結束,即便研究結果和預測的方向完全相反,也應該虛心接受,並保留虛無假設。
以上為本篇文章對於顯著水準和決策規則的介紹,希望透過本篇文章,您瞭解了顯著水準的意義、決策規則的使用以及顯著水準和研究假設方向性有無之間的關聯。
若您喜歡本篇文章,請將本網站加入書籤,作為您的學習資源,並持續回訪本網站喔!另外,您也可以在Facebook和Twitter上找到我們喲!
參考資料
Ruxton, G. D, & Neuhäuser, M. (2010). When should we use one-tailed hypothesis testing? Methods in Ecology and Evolution, 1, 114-117. https://doi.org/10.1111/j.2041-210X.2010.00014.x